

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Groups
المؤلف:
Tony Crilly
المصدر:
50 mathematical ideas you really need to know
الجزء والصفحة:
219-224
23-2-2016
1932
Evariste Galois died in a duel aged 20, but left behind enough ideas to keep mathematicians busy for centuries. These involved the theory of groups, mathematical constructs that can be used to quantify symmetry. Apart from its artistic appeal, symmetry is the essential ingredient for scientists who dream of a future theory of everything. Group theory is the glue which binds the ‘everything’ together.
Symmetry is all around us. Greek vases have it, snow crystals have it, buildings often have it and some letters of our alphabet have it. There are several sorts of symmetry: chief among them are mirror symmetry and rotational symmetry. We’ll just look at two-dimensional symmetry – all our objects of study live on the flat surface of this page.
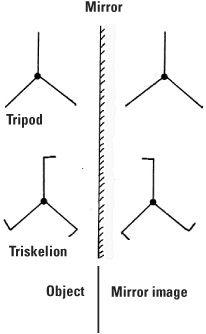
Mirror symmetry
Can we set up a mirror so that an object looks the same in front of the mirror as in the mirror? The word MUM has mirror symmetry, but HAM does not; MUM in front of the mirror is the same as MUM in the mirror while HAM becomes MAH. A tripod has mirror symmetry, but the triskelion (tripod with feet) does not. The triskelion as the object before the mirror is right-handed but its mirror image in what is called the image plane is left-handed.
Rotational symmetry
We can also ask whether there is an axis perpendicular to the page so that the object can be rotated in the page through an angle and be brought back to its original position. Both the tripod and the triskelion have rotational symmetry. The triskelion, meaning ‘three legs’, is an interesting shape. The right-handed version is a figure which appears as the symbol of the Isle of Man and also on the flag of Sicily.
If we rotate it through 120 degrees or 240 degrees the rotated figure will coincide with itself; if you closed your eyes before rotating it you would see the same triskelion when you opened them again after rotation.
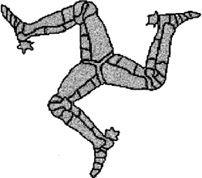
The Isle of Man triskelion
The curious thing about the three-legged figure is that no amount of rotation keeping in the plane will ever convert a right-handed triskelion into a left-handed one. Objects for which the image in the mirror is distinct from the object in front of the mirror are called chiral – they look similar but are not the same. The molecular structure of some chemical compounds may exist in both right-handed and left-handed forms in three dimensions and are examples of chiral objects. This is the case with the compound limosene which in one form tastes like lemons and in the other like oranges. The drug thalidomide in one form is an effective cure of morning sickness in pregnancy but in the other form has tragic consequences.
Measuring symmetry
In the case of our triskelion the basic symmetry operations are the (clockwise) rotations R through 120 degrees and S through 240 degrees. The transformation I is the one that rotates the triangle through 360 degrees or, alternatively, does nothing at all. We can create a table based on the combinations of these rotations, in the same way we might create a multiplication table.

Cayley table for the symmetry group of the triskelion
This table is like an ordinary multiplication table with numbers except we are ‘multiplying’ symbols. According to the most widely used convention, the multiplication R ° S means first rotate the triskelion clockwise through 240 degrees with S and then by 120 degrees with R, the result being a rotation by 360 degrees, as if you did nothing at all. This can be expressed as R ° S = I, the result found at the junction of the last but one row and the last column of the table.
The symmetry group of the triskelion is made up of I, R and S and the multiplication table of how to combine them. Because the group contains three elements its size (or ‘order’) is three. The table is also called a Cayley table (named after the mathematician Arthur Cayley, distant cousin to Sir George Cayley a pioneer of flight).

Caley table for the symmetry group of the tripod
Like the triskelion, the tripod without feet has rotational symmetry. But it also has mirror symmetry and therefore has a larger symmetry group. We’ll call U, V and W the reflections in the three mirror axes.
The larger symmetry group of the tripod, which is of order six, is composed of the six transformations I, R, S, U, V and W and has the multiplication table shown.
An interesting transformation is achieved by combining two reflections in different axes, such as U ° W (where the reflection W is applied first and is followed by the reflection U). This is actually a rotation of the tripod through 120 degrees, in symbols U ° W = R. Combining the reflections the other way around W ° U = S, gives a rotation through 240 degrees. In particular U ° W ≠ W ° U. This is a major difference between a multiplication table for a group and an ordinary multiplication table with numbers.
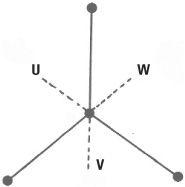
Reflections of a tripod
A group in which the order of combining the elements is immaterial is called an abelian group, named after the Norwegian mathematician Niels Abel. The symmetry group of the tripod is the smallest group which is not abelian.
Abstract groups
The trend in algebra in the 20th century had been towards abstract algebra, in which a group is defined by some basic rules known as axioms. With this viewpoint the symmetry group of the triangle becomes just one example of an abstract system. There are systems in algebra that are more basic than a group and require fewer axioms; other systems that are more complex require more axioms. However the concept of a group is just right and is the most important algebraic system of all. It is remarkable that from so few axioms such a large body of knowledge has emerged. The advantage of the abstract method is that general theorems can be deduced for all groups and applied, if need be, to specific ones.
A feature of group theory is that there may be small groups sitting inside bigger ones. The symmetry group of the triskelion of order three is a subgroup of the symmetry group of the tripod of order six. J.L. Lagrange proved a basic fact about subgroups. Lagrange’s theorem states that the order of a subgroup must always divide exactly the order of the group. So we automatically know the symmetry group of the tripod has no subgroups of order four or five.
Classifying groups
There has been an extensive programme to classify all the possible finite groups. There is no need to list them all because some groups are built up from basic ones, and it is the basic ones that are needed. The principle of classification is much the same as in chemistry where interest is focused on the basic chemical elements and not the compounds which can be made from them. The symmetry group of the tripod of six elements is a ‘compound’ being built up from the group of rotations (of order three) and reflections (of order two).
Axioms for a group
A collection of elements G with ‘multiplication’ ° is called a group if
1. There is an element 1 in G so that 1 ° = a ° 1 = a for all elements a in the group G (the special element 1 is called the identity element).
2. For each element a in G there is an element ā in G with ā ° a = a ° ā = 1 (the element ā is called the inverse element of a).
3. For all elements a, b and c in G it is true that a ° (b ° c) = (a ° b) ° c (this is called the associative law).
Nearly all basic groups can be classified into known classes. The complete classification, called ‘the enormous theorem’, was announced by Daniel Gorenstein in 1983 and was arrived at through the accumulated work of 30 years’ worth of research and publications by mathematicians. It is an atlas of all known groups. The basic groups fall into one of four main types, yet 26 groups have been found that do not fall into any category. These are known as the sporadic groups.
The sporadic groups are mavericks and are typically of large order. Five of the smallest were known to Emile Mathieu in the 1860s but much of the modern activity took place between 1965 and 1975. The smallest sporadic group is of order 7920 = 24 × 32 × 5 × 11 but at the upper end are the ‘baby monster’ and the plain ‘monster’ which has order 246 × 320 × 59 × 76 × 112 × 133 × 17 × 19 × 23 × 29 × 31 × 41 × 47 × 59 × 71 which in decimal speak is around 8 × 1053 or, if you like, 8 with 53 trailing zeros – a very large number indeed. It can be shown that 20 of the 26 sporadic groups are represented as subgroups inside the ‘monster’ – the six groups that defy all classificatory systems are known as the ‘six pariahs’.
Although snappy proofs and shortness are much sought after in mathematics, the proof of the classification of finite groups is something like 10,000 pages of closely argued symbolics. Mathematical progress is not always due to the work of a single outstanding genius.
the condensed idea
Measuring symmetry

 الاكثر قراءة في هل تعلم
الاكثر قراءة في هل تعلم
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















