The theory of relativity was set out by the Dutch physicist Hendrik Lorentz in the late 19th century, but the definitive advance was made by Albert Einstein in 1905. Einstein’s famous paper on special relativity revolutionized the study of how objects move, reducing Newton’s classical theory, a magnificent achievement in its time, to a special case.

Back to Galileo

To describe the theory of relativity we take a tip from the master himself: Einstein loved to talk about railway trains and thought experiments. In our example, Jim Diamond is on board a train travelling at 60 mph. From his seat at the back of the train he walks towards the cafeteria car at 2 mph. His speed is 62 mph relative to the ground. On returning to his seat Jim’s speed relative to the ground will be 58 mph because he is walking in the opposite direction to the train’s travel. This is what Newton’s theory tells us. Speed is a relative concept and Jim’s direction of motion determines whether you add or subtract.

Because all motion is relative, we talk about a ‘frame of reference’ as the viewpoint from which a particular motion is measured. In the one-dimensional motion of the train moving along a straight track we can think of a fixed frame of reference positioned at a railway station and a distance x and a time t in terms of this reference frame. The zero position is determined by a point marked on the platform and the time read from the station clock. The distance/time coordinates relative to this reference frame at the station are (x, t).

There is also a reference frame on board the train. If we measure distance from the end of the train and time by Jim’s wristwatch there would be another set of coordinates 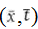. It is also possible to synchronize these two coordinate systems. When the train passes the mark on the platform, then x = 0 and the station clock is at t = 0. If Jim sets x= 0 at this point, and puts t= 0 on his wristwatch, there is now a connection between these coordinates.

As the train passes through the station Jim sets off for the cafeteria car. We can calculate how far he is from the station after five minutes. We know that the train is travelling at 1 mile per minute, so in that time it has travelled 5 miles and Jim has walked 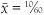of a mile (from his speed of 2 mph multiplied by time 5/60). So in total Jim is a distance (x) which is 510/60 miles from the station. The relation between x and t is therefore given by x = x+ v × t (here v = 60). Turning the equation around to give the distance Jim has travelled relative to the reference frame on the train, we get

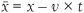
The concept of time in the classical Newtonian theory is a one-dimensional flow from the past to the future. It is universal for all and it is independent of space. Since it is an absolute quantity, Jim’s time on board the train is the same for the station master on the platform t, so

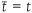
These two formulae for xand t, first derived by Galileo, are types of equations called transformations, as they transform quantities from one reference frame to another. According to Newton’s classical theory, the speed of light should be expected to obey these two Galilean transformations for xand t.

By the 17th century people recognized that light had speed, and its approximate value was measured in 1676 by the Danish astronomer Ole Römer. When Albert Michelson measured the speed of light more accurately in 1881, he found it was 186,300 miles per second. More than this, he became aware that the transmission of light was very different from the transmission of sound. Michelson found that, unlike the speed of our observer on the moving train, the direction of the light beam had no bearing on the speed of light at all. This paradoxical result had to be explained.

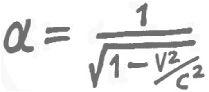
The Lorentz factor

The special theory of relativity

Lorentz set out the mathematical equations which governed the connection between the distance and time when one frame of reference moves at a constant speed v relative to another. These transformations are very similar to the ones we have already worked out but involve a (Lorentz) factor depending on v and the speed of light, c.

Enter Einstein

The way Einstein dealt with Michelson’s findings about the speed of light was to adopt it as a postulate:

The speed of light is the same value for all observers and is independent of direction.

If Jim Diamond flicked a torch on and off while passing through the station on his speeding train, firing the light beam down the carriage in the direction the train was moving, he would measure its speed as c. Einstein’s postulate says that the watching stationmaster on the platform would also measure the beam’s speed as c, not as c + 60 mph. Einstein also assumed a second principle:

One frame of reference moves with constant speed in relation to another.

The brilliance of Einstein’s 1905 paper was due in part to the way he approached his work, being motivated by mathematical elegance. Sound waves travel as vibrations of molecules in the medium through which the sound is being carried. Other physicists had assumed light also needed some medium to travel through. No one knew what it was, but they gave it a name – the luminiferous aether.

Einstein felt no need to assume the existence of the aether as the medium for transmitting light. Instead, he deduced the Lorentz transformations from the two simple principles of relativity and the whole theory unfolded. In particular, he showed that the energy of a particle E is determined by the equation

E = ×mc². For the energy of a body at rest (when v = 0 and so = 1), this leads to the iconic equation showing that mass and energy are equivalent:

E = mc²

Lorentz and Einstein were both proposed for the Nobel Prize in 1912. Lorentz had already been given it in 1902, but Einstein had to wait until 1921 when he was finally awarded the prize for work on the photoelectric effect (which he had also published in 1905). That was quite a year for the Swiss patent clerk.

Einstein vs Newton

For observations on slow moving railway trains there is only a very small difference between Einstein’s relativity theory and the classical Newtonian theory. In these situations the relative speed v is so small compared with the speed of light that the value of the Lorentz factor α is almost 1. In this case the Lorentz equations are virtually the same as the classical Galilean transformations. So for slow speeds Einstein and Newton would agree with each other. Speeds and distances have to be very large for the differences between the two theories to be apparent. Even the record breaking French TGV train has not reached these speeds yet and it will be a long time in the development of rail travel before we would have to discard the Newtonian theory in favour of Einstein’s. Space travel will force us to go with Einstein.

The general theory of relativityEinstein published his general theory in 1915. This theory applies to motion when frames of reference are allowed to accelerate in relation to each other and links the effects of acceleration with those of gravity.

Using the general theory Einstein was able to predict such physical phenomena as the deflection of light beams by the gravitational fields of large objects such as the Sun. His theory also explained the motion of the axis of Mercury’s rotation. This precession could not be fully explained by Newton’s theory of gravitation and the force exerted on Mercury by the other planets. It was a problem that had bothered astronomers since the 1840s.

The appropriate frame of reference for the general theory is that of the four-dimensional space–time. Euclidean space is flat (it has zero curvature) but Einstein’s four-dimensional space–time geometry (or Riemannian geometry) is curved. It displaces the Newtonian force of gravity as the explanation for objects being attracted to each other. With Einstein’s general theory of relativity it is the curvature of space–time which explains this attraction. In 1915 Einstein launched another scientific revolution.

the condensed idea

The speed of light is absolute

a