

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
The Riemann hypothesis
المؤلف:
Tony Crilly
المصدر:
50 mathematical ideas you really need to know
الجزء والصفحة:
282-286
28-2-2016
4115
The Riemann hypothesis represents one of the stiffest challenges in pure mathematics. The Poincaré conjecture and Fermat’s last theorem have been conquered but not the Riemann hypothesis. Once decided, one way or the other, elusive questions about the distribution of prime numbers will be settled and a range of new questions will be opened up for mathematicians to ponder.
The story starts with the addition of fractions of the kind

The answer is 1⅚ (approximately 1.83). But what happens if we keep adding smaller and smaller fractions, say up to ten of them?

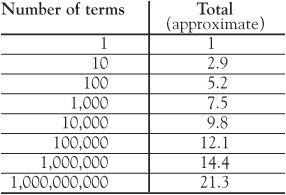
Using only a handheld calculator, these fractions add up to approximately 2.9 in decimals. A table shows how the total grows as more and more terms are added.
The series of numbers
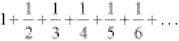
is called the harmonic series. The harmonic label originates with the Pythagoreans who believed that a musical string divided by a half, a third, a quarter, gave the musical notes essential for harmony.
In the harmonic series, smaller and smaller fractions are being added but what happens to the total? Does it grow beyond all numbers, or is there a barrier somewhere, a limit that it never rises above? To answer this, the trick is to group the terms, doubling the runs as we go. If we add the first 8 terms (recognizing that 8 = 2 × 2 × 2 = 23) for example
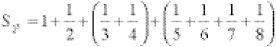
(where S stands for sum) and, because ⅓ is bigger than ¼ and ⅕ is bigger than ⅛ (and so on), this is greater than
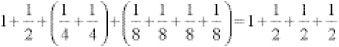
So we can say

and more generally
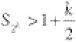
If we take k = 20, so that n = 220 = 1,048,576 (more than a million terms), the sum of the series will only have exceeded 11 (see table). It is increasing in an excruciatingly slow way – but, a value of k can be chosen to make the series total beyond any preassigned number, however large. The series is said to diverge to infinity. By contrast, this does not happen with the series of squared terms
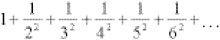
We are still using the same process: adding smaller and smaller numbers together, but this time a limit is reached, and this limit is less than 2. Quite dramatically the series converges to π2/6 = 1.64493 . . .
In this last series the power of the terms is 2. In the harmonic series the power of the denominators is silently equal to 1 and this value is critical. If the power increases by a minuscule amount to a number just above 1 the series converges, but if the power decreases by a minuscule amount to a value just below 1, the series diverges. The harmonic series sits on the boundary between convergence and divergence.
The Riemann zeta function
The celebrated Riemann zeta function ζ(s) was actually known to Euler in the 18th century but Bernhard Riemann recognized its full importance. The ζ is the Greek letter zeta, while the function is written as:
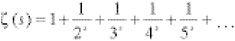
Various values of the zeta function have been computed, most prominently, ξ(1) = ∞ because ξ(1) is the harmonic series. The value of ξ(2) is π2/6, the result discovered by Euler. It has been shown that the values of ξ(s) all involve π when s is an even number while the theory of ξ(s) for odd values of s is far more difficult. Roger Apéry proved the important result that ξ(3) is an irrational number but his method did not extend to ξ(5), ξ(7), ξ(9), and so on.
The Riemann hypothesis
The variable s in the Riemann zeta function represents a real variable but this can be extended to represent a complex number . This enables the powerful techniques of complex analysis to be applied to it.
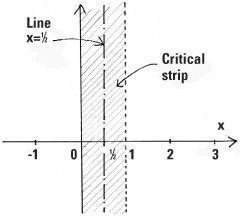
The Riemann zeta function has an infinity of zeros, that is, an infinity of values of s for which ξ(s) = 0. In a paper presented to the Berlin Academy of Sciences in 1859, Riemann showed all the important zeros were complex numbers that lay in the critical strip bounded by x = 0 and x = 1. He also made his famous hypothesis:
All the zeros of the Riemann zeta function ξ(s) lie on the line x = ½; the line along the middle of the critical strip.
The first real step towards settling this hypothesis was made in 1896 independently by Charles de la Vallée-Poussin and Jacques Hadamard. They showed that the zeros must lie on the interior of the strip (so x could not equal 0 or 1). In 1914, the English mathematician G.H. Hardy proved that an infinity of zeros lie along the line x = ½ though this does not prevent there being an infinity of zeros lying off it.
As far as numerical results go, the non-trivial zeros calculated by 1986 (1,500,000,000 of them) do lie on the line x = ½ while up-to-date calculations have verified this is also true for the first 100 billion zeros. While these experimental results suggest that the conjecture is reasonable, there is still the possibility that it may be false. The conjecture is that all zeros lie on this critical line, but this awaits proof or disproof.
Why is the Riemann hypothesis important?
There is an unexpected connection between the Riemann zeta function ξ (s) and the theory of prime numbers . The prime numbers are 2, 3, 5, 7, 11 and so on, the numbers only divisible by 1 and themselves. Using primes, we can form the expression

and this turns out to be another way of writing ξ(s), the Riemann zeta function. This tells us that knowledge of the Riemann zeta function will throw light on the distribution of prime numbers and enhance our understanding of the basic building blocks of mathematics.
In 1900, David Hilbert set out his famous 23 problems for mathematicians to solve. He said of his eighth problem, ‘if I were to awaken after having slept for five hundred years, my first question would be: Has the Riemann hypothesis been proven?’
Hardy used the Riemann hypothesis as insurance when crossing the North sea after his summer visit to his friend Harald Bohr in Denmark. Before leaving port he would send his friend a postcard with the claim that he had just proved the Riemann hypothesis. It was a clever each way bet. If the boat sank he would have the posthumous honour of solving the great problem. On the other hand, if God did exist he would not let an atheist like Hardy have that honour and would therefore prevent the boat from sinking.
The person who can rigorously resolve the issue will win a prize of a million dollars offered by the Clay Mathematics Institute. But money is not the driving force – most mathematicians would settle for achieving the result and a very high position in the pantheon of great mathematicians.
the condensed idea
The ultimate challenge

 الاكثر قراءة في هل تعلم
الاكثر قراءة في هل تعلم
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















