
Triangles
 المؤلف:
Tony Crilly
المؤلف:
Tony Crilly
 المصدر:
50 mathematical ideas you really need to know
المصدر:
50 mathematical ideas you really need to know
 الجزء والصفحة:
118-124
الجزء والصفحة:
118-124
 28-2-2016
28-2-2016
 2347
2347
The most obvious fact about a triangle is that it is a figure with three sides and three angles (tri-angles). Trigonometry is the theory which we use to ‘measure the triangle’, whether it is the size of the angles, the length of the sides, or the enclosed area. This shape – one of the simplest of all figures – is of enduring interest.
The triangle’s tale
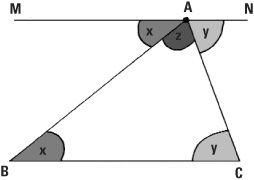
There is a neat argument to show that the angles in any triangle add up to two right angles or 180 degrees. Through the point or ‘vertex’ A of any triangle draw a line MAN parallel to the base BC.
The angle A  C which we’ll call x is equal to the angle BÂM because they are alternate angles and MN and BC are parallel. The other two alternate angles are equal to y. The angle about the point A is equal to 180 degrees (half of 360 degrees) and this is x + y + z which is the sum of the angles in the triangle. QED as was often written at the end of his proofs. Of course we are assuming the triangle is drawn on a flat surface like this flat piece of paper. The angles of a triangle drawn on a ball (a spherical triangle) do not add up to 180 degrees but that is another story.
C which we’ll call x is equal to the angle BÂM because they are alternate angles and MN and BC are parallel. The other two alternate angles are equal to y. The angle about the point A is equal to 180 degrees (half of 360 degrees) and this is x + y + z which is the sum of the angles in the triangle. QED as was often written at the end of his proofs. Of course we are assuming the triangle is drawn on a flat surface like this flat piece of paper. The angles of a triangle drawn on a ball (a spherical triangle) do not add up to 180 degrees but that is another story.
Euclid proved many theorems about triangles, always making sure this was done deductively. He showed, for example, that ‘in any triangle two sides taken together in any manner are greater than the remaining one’. Nowadays this is called the ‘triangle inequality’ and is important in abstract mathematics. The Epicureans, with their down-to-earth approach to life, claimed this required no proof, for it was evident even to an ass. If a bale of hay were placed at one vertex and the ass at the other, they argued, the animal would hardly traverse the two sides to satisfy its hunger.
Pythagoras’s theorem
The greatest triangle theorem of all is Pythagoras’s theorem, and is one which features in modern mathematics – though there is some doubt about Pythagoras being the first to discover it. The best known statement of it is in terms of algebra, a2 + b2 = c2 but Euclid refers to actual square shapes: ‘In right-angled triangles the square on the side subtending the right angle is equal to the squares on the sides containing the right angle’.

Euclid’s proof is Proposition 47, in Book 1 of the Elements, a proof which became a point of anxiety for generations of school pupils as they struggled to commit it to memory, or take the consequences. There are several hundred proofs in existence. A favourite is more in the spirit of Bhāskara of the 12th century than a Euclidean proof from 300 BC.
This is a proof ‘without words’. In the figure the square with side a + b can be divided in two different ways.
Since the four equal triangles (shaded dark) are common to both squares we can remove them and still have equality of area. If we look at the areas of the remaining shapes, out springs the familiar expression.
a2 + b2 = c2
The Euler line
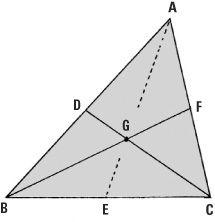
Hundreds of propositions about triangles are possible. First, let’s think about the midpoints of the sides. In any triangle ABC we mark the midpoints D, E, F of its sides. Join B to F and C to D and mark the point where they cross as G. Now join A to E. Does this line also pass through G? It is not obvious that it should necessarily without further reasoning. It fact it does and the point G is called the ‘centroid’ of the triangle. This is the centre of gravity of the triangle.
There are literally hundreds of different ‘centres’ connected with a triangle. Another one is the point H where the altitudes meet. This is called the ‘orthocentre’. There is also another centre called the ‘circumcentre’ O where each of the lines (known as ‘perpendiculars’) at D, E and F meet (not shown). This is the centre of the circle which can be drawn through A, B and C.
But more is true. In any triangle ABC the centres G, H and O, respectively the centroid, orthocentre, and circumcentre, themselves lie along one line, called the ‘Euler line’. In the case of an equilateral triangle (all sides of equal length) these three points coincide and the resulting point is unambiguously the centre of the triangle.
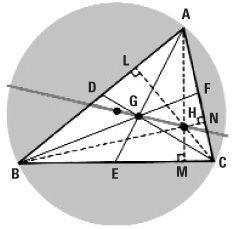
The Euler line
Napoleon’s theorem
For any triangle ABC, equilateral triangles can be constructed on each side and from their centres a new triangle DEF is constructed. Napoleon’s theorem asserts that for any triangle ABC, the triangle DEF is an equilateral triangle.
Napoleon’s theorem appeared in print in an English journal in 1825 a few years after his death on St Helena in 1821. Napoleon’s ability in mathematics in school no doubt helped him gain entrance to the artillery school, and later he got to know the leading mathematicians in Paris when he was Emperor. Unfortunately there is no evidence to take us further and ‘Napoleon’s theorem’ is, like many other mathematical results, ascribed to a person who had little to do with its discovery or its proof. Indeed, it is a theorem which is frequently being rediscovered and extended.
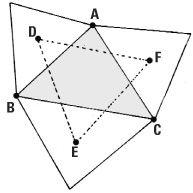
Napoleon’s theorem
The essential data that determines a triangle consists of knowing the length of one side and two angles. By using trigonometry we can measure everything else.
In surveying areas of land in order to draw maps it is quite useful to be a ‘flat-earther’ and assume triangles to be flat. A network of triangles is established by starting with a base line BC of known length, choosing a distant point A (the triangulation point) and measuring the angles A  C and AĈB by theodolite. By trigonometry everything is known about the triangle ABC and the surveyor moves on, fixes the next triangulation point from the new base line AB or AC and repeats the operation to establish a web of triangles. The method has the advantage of being able to map inhospitable country involving such barriers as marshland, bogs, quicksand and rivers.
C and AĈB by theodolite. By trigonometry everything is known about the triangle ABC and the surveyor moves on, fixes the next triangulation point from the new base line AB or AC and repeats the operation to establish a web of triangles. The method has the advantage of being able to map inhospitable country involving such barriers as marshland, bogs, quicksand and rivers.
It was used as the basis for the Great Trigonometrical Survey of India which began in the 1800s and lasted 40 years. The object was to survey and map along the Great Meridional Arc from Cape Comorin in the south to the Himalayas in the north, a distance of some 1500 miles. To ensure utmost accuracy in measuring angles, Sir George Everest arranged the manufacture of two giant theodolites in London, together weighing one ton and needing teams of a dozen men to transport them. It was vital to get the angles right. Accuracy in measurement was paramount and much talked about but it was the humble triangle which was at the centre of operations. The Victorians had to make do without GPS though they did have computers – human computers. Once all the lengths in a triangle have been computed, the calculation of area is straightforward. Once again, the triangle is the unit. There are several formulae for the area A of a triangle, but the most remarkable is Heron of Alexandria’s formula:
Building with triangles
The triangle is indispensable in building. Its use and strength relies on the fact that made it indispensable in surveying – a triangle is rigid. You can push a square or rectangle out of shape but not a triangle. The truss used in building is the joining together of triangles, and is seen as the component in roofs. One breakthrough occurred in the building of bridges.
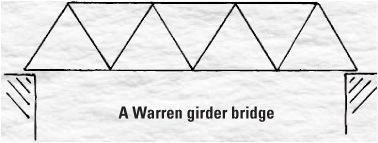
A Warren girder bridge
A Warren truss can take a heavy loading compared to its weight. It was patented in 1848 by James Warren and the first bridge designed in this way was constructed at London Bridge Station two years later. The use of equilateral triangles proved more reliable than similar designs based on the isosceles triangles, the triangles where only two sides are required to be equal.
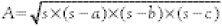
It can be applied to any triangle and we don’t even have to know any angles. The symbol s stands for one half of the perimeter of the triangle whose sides are of length a, b and c. For example, if a triangle has sides 13, 14 and 15, the perimeter is 13 + 14 + 15 = 42, so that s = 21. Completing the calculation, 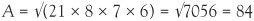 . The triangle is a familiar object, whether to children playing with simple shapes or researchers dealing on a day-to-day basis with the triangle inequality in abstract mathematics. Trigonometry is the basis for making calculations about triangles and the sine, cosine and tangent functions are the tools for describing them, enabling us to make accurate calculations for practical applications. The triangle has received much attention but it is surprising that so much is waiting to be discovered about three lines forming such a basic figure.
. The triangle is a familiar object, whether to children playing with simple shapes or researchers dealing on a day-to-day basis with the triangle inequality in abstract mathematics. Trigonometry is the basis for making calculations about triangles and the sine, cosine and tangent functions are the tools for describing them, enabling us to make accurate calculations for practical applications. The triangle has received much attention but it is surprising that so much is waiting to be discovered about three lines forming such a basic figure.
the condensed idea
Three sides of a story

 الاكثر قراءة في هل تعلم
الاكثر قراءة في هل تعلم
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


