LASER   GAIN

Assuming that we’ve generated population inversion (by pumping energy into the lasing medium, in this example a gas, to excite upper lasing levels), laser gain may now occur. Laser gain (or optical gain) is a measure of how well a medium amplifies photons by stimulated emission. Consider a single photon traveling down a laser tube and stimulating an excited atom to emit a photon of the same frequency and phase this is laser gain. Thinking of the stream of photons traveling down the tube as an electromagnetic wave, we can see that the power of the wave increases if the rate of stimulated emissions exceeds that of spontaneous emissions. As the wave travels farther down the tube, the power increases as a function of length. The power increase, mathematically, is

exp(gx)    (1.1)

where g is the optical gain coefficient of the laser medium and x is the distance down the tube. No surprises, the power increases exponentially as the wave travels down the tube. Consider where one photon stimulates another, giving us two; these two then stimulate two more, so we get four, and so on. The exponential nature of this gain is evident. The gain coefficient, g, represents the optical power gain per unit length. Mathematically, it can be expressed as ΔP/Δx, the change in power for a given length of lasing medium, or more correctly,

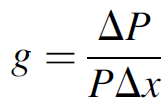 (1.2)

which yields a quantity in units of length^-1 (e.g., m^-1). The standard model for picturing a gain medium, shown in Figure 1.1, is to view a thin slice of a medium.

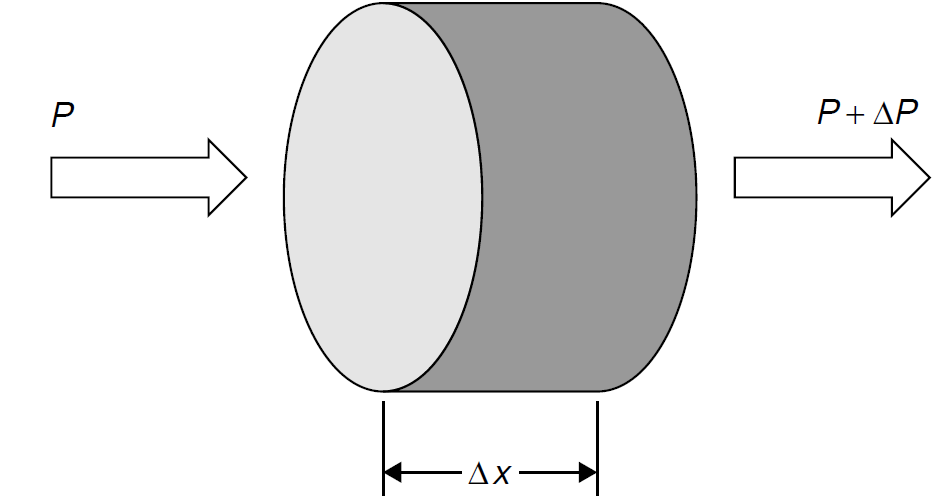
Figure 1.1. Gain in a laser medium.

       A stream of photons with power P enters the gain medium, which has length Δx, and exits with increased power P+ΔP. Gain is proportional to the net rate of stimulated emission, which is in turn equal to the rate of stimulated emission minus the rate of absorption. The ramifications for practical laser construction are simple: The longer the lasing medium, the more power will increase per pass down the tube. When attempting to lase a weak transition (as many gases have), a longer tube will allow a larger power increase per pass through the tube. This may be important when considering losses in the laser.

      The gain of a laser may be expressed in various ways, such as percent per pass, percent per meter, or m^-1. As an example, consider an ion laser tube 80 cm long with a gain of 12% per pass. Each time the beam traverses the gain medium (the laser tube) it gains 12% in power. This gain may also be expressed as 15% per meter (12%/0.8 m), or 0.15 m^-1. Although this figure may seem high, and it is for many lasers, consider losses in the laser that must be overcome. Assuming that we use aluminum mirrors, which reflect about 85% of incident light, this laser cannot work. The loss at one mirror alone (15% loss) is greater than the gain down the entire tube! Total losses in the laser, including the portion we extract as our output beam, losses in the mirrors, losses at the tube windows, and absorption (or reabsorption) within the tube itself, cannot exceed 12% in this case. Clearly, laser cavities must be designed for minimal loss.

Example 1.1 Laser Gain Calculation Consider a small pulsed mercury-ion laser (with output in the green) which has a tube 0.1 m long and a gain of 50% per meter. The gain in this particular laser is exceedingly large; few other gas lasers have gains of 50% per meter! Assume that the total reflector has a loss of 0.1% (these are special, dielectric mirrors). Most ion lasers have Brewster windows; in this case, assume that each has a loss of 0.8%. Finally, the tube has an attenuation of 0.1 m21. The parameters are included in Figure 1.2. Given these parameters, calculate the maximum transmission, in percent, that can be extracted through one of the mirrors as an output beam.

Figure 1.2. Gain and loss in a mercury-ion laser.

SOLUTION To solve this, sum the total loss in the laser on a round trip through the tube. Radiation in the cavity passes down the tube, being amplified 5% (50% × 0.1 m) in the single pass. At the same time, the pass down the tube also attenuates the power by 1% (this is absorption in the tube and will be discussed shortly). In this case the attenuation is specified as 0.1 m^-1 (0.1 per meter) or 1.0% per pass for the 0.1-m tube length. Passing through the Brewster window the beam loses 0.8%. Another 0.1% is lost at the total reflector, and another 0.8% as the beam passes once more through the window to reenter the tube. The situation is repeated as the beam is amplified and a loss occurs at the other end of the tube, where the beam reflects off the output coupler.

     Total loss is calculated as 1% (attenuation during forward pass)‏+ 0.8% (exiting the tube via the window) +‏ 0.1% (total reflector loss) ‏+ 0.8% (entering the tube)‏ +1% (attenuation) ‏+ 0.8% (exiting the tube) ‏+ 0.8% (entering the tube) = 5.3%. Total gain is calculated as two passes of 5% each, or 10%. We could then extract 10-5.3 = 4.7% as an output beam (the output coupler could impose a loss of 4.7%, which includes losses in the mirror itself plus the portion transmitted). This would not be optimal, however, as it barely allows the laser to oscillate. In reality, the output transmission of the mirror would be designed to be about 2.0%, to ensure that the energy density inside the cavity is more than enough to sustain laser action. It is also obvious why certain features of real lasers are designed the way they are. First, the mirrors in almost all lasers are dielectric types. Ordinary aluminized mirrors reflect only 85% of the incident light; such losses are not tolerable in a system like this. The second feature of many lasers are the angled Brewster windows on the tube ends. From basic optics theory you will recall that at a specific angle a window will have almost zero loss to a certain polarity of light. Ordinary, uncoated glass windows perpendicular to incident light have a reflective loss of about 8%. Again, such losses from a plane window on a plasma tube are not tolerable in most lasers, so windows at Brewster angles or windows with special antireflective coatings are required.

       So the requirements for laser oscillation are not solely that population inversion occurs (i.e., the population of atoms at the upper lasing level exceeds that at the lower level) but also that the gain be high enough to overcome any losses in the cavity. These losses include the portion we extract as an output beam. The required laser gain also depends on the inverse of the spontaneous lifetime of the lasing medium. A long lifetime implies that less gain is needed. This is reasonable considering that a longer lifetime allows excited atoms to stay in the upper lasing level longer, giving them better odds of being stimulated into emitting laser light before spontaneously emitting a (useless) photon. Again, this is examined in detail later.