


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 24-7-2016
التاريخ: 27-4-2016
التاريخ: 2023-07-02
التاريخ: 2024-02-25
|
امتصاص وانبعاث الفوتون
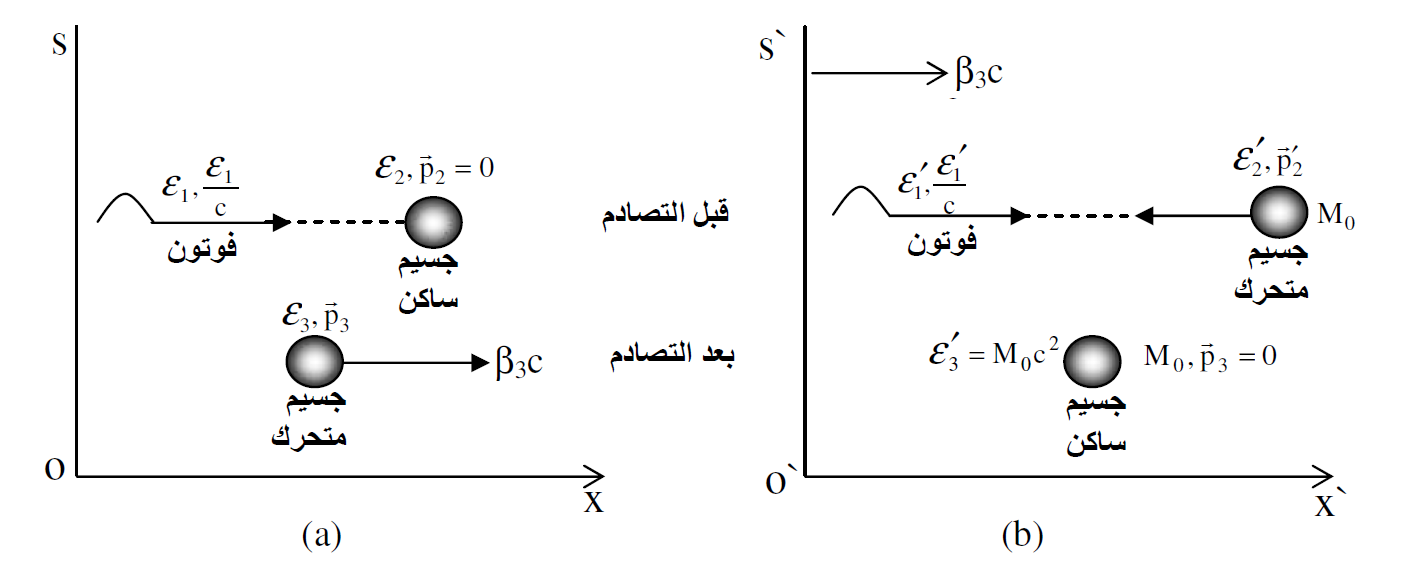
الشكل (1.1) : (a) امتصاص فوتون عند منقوطه على جسيم في حالة سكون. (b) امتصاص فوتون حيث يكون الزخم الكلي مساويا صفرا خلال عملية الامتصاص.
اولا: الامتصاص
لنفرض ان لدينا جسيما في حالة سكون (ذرة او نواة) كتلته الساكنة M0، سقط عليه فوتون طاقته 1ε في محور الاسناد s وتم امتصاصه كليا بواسطة هذا الجسيم. وقد اكتسب الجسيم الجديد بعد عملية الامتصاص سرعة تساوي 3cβ وطاقة كلية تساوي ε = M0 c2 = γM0 c2
حيث ان : 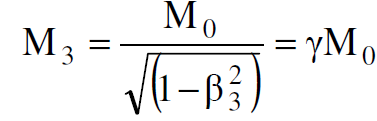
كما موضح في الشكل (1.1a). اما الكتلة الساكنة فبقيت دون تغيير قبل وبعد عملية الامتصاص وتساوي ..
علينا الان ان نحسب 3β للجسيم الجديد باستخدام محاور الاسناد وقوانين حفظ الزخم والطاقة بفرض ان عملية الامتصاص هذه هي تصادم مرن وتام. في محور الاسنادsʹ نلاحظ في الشكل (1.1b) انه يتحرك بسرعة ثابتة تساوي 3cβ.
إذن يكون التصادم في هذا المحور محفوظًا وان الزخم الكلي للنظام يساوي صفرا قبل وبعد التصادم. نطبق الان قانون حفظ الطاقة والزخم في s فيكون :
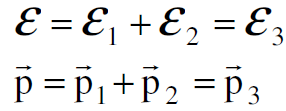
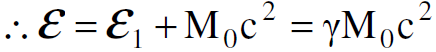 (1.1)
(1.1)
نطبق مرة اخرى قانون حفظ الزخم والطاقة في sʹ فيكون :
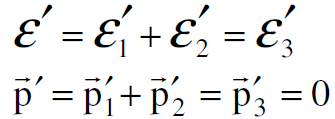
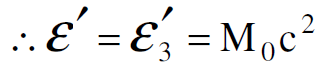 (1.2)
(1.2)
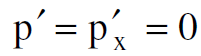
وباستخدام معادلة تحويل الزخم من sʹ الى s نحصل على :
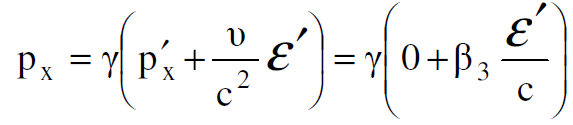
حيث ان 3=v/cβ
وبما ان :
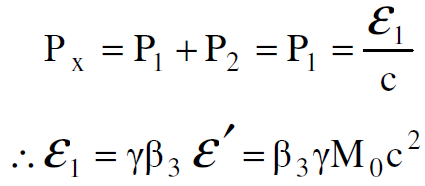
وبالاستعانة بالعلاقة (1.1) ينتج ان :
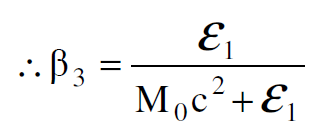
واذا فرضنا ان >>ε1 M0c2 يكون :
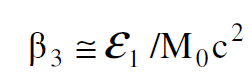
نستنتج من هذا ان الجسيم الذي تبقى كتلته دون تغيير خلال عملية الامتصاص يعطى دفا من قبل الفوتون يساوي ε1/c على فرض ان الكتلة M0 لا تتغير خلال التصادم كما هي الحال في ميكانيك نيوتن.
ثانيا: الانبعاث
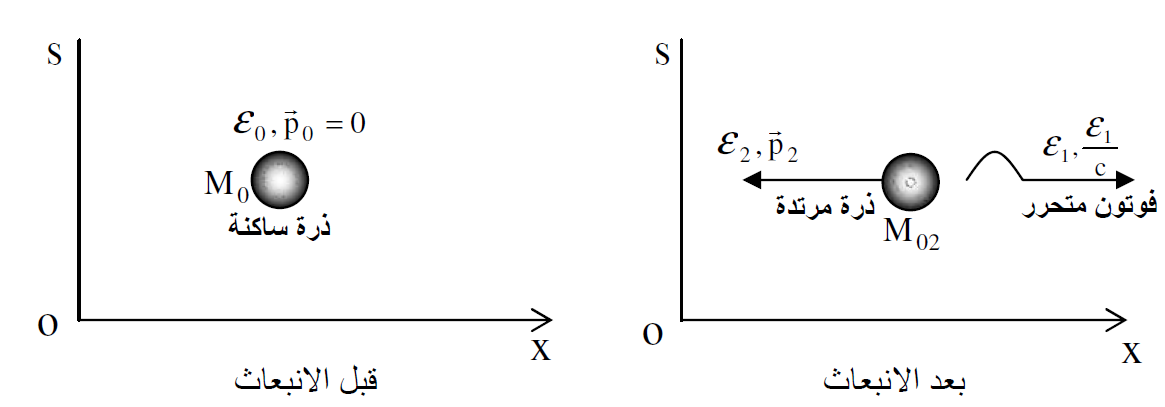
الشكل (1.2) : انبعاث فوتون من جسيم في حالة سكون. يحدث تغيرا في الكتلة الساكنة للجسيم بعد الانبعاث.
لنعتبر الان ان ذرة ساكنة كتلتها السكونية M0 وطاقتها 0ε انبعث منها فوتون طاقته ε1 هذه الحالة اكثر تعقيدا لان الذرة تعاني ارتدادا بزخم p2 وبطاقة كلية ε2 وينتج عن هذا تغير في الكتلة الساكنة الى M02 لاحظ الشكل (1.2) قبل وبعد الانبعاث.
يستخدم هنا محور اسناد واحد هو s الذي يمثل ايضا المحاور المختبرية وليس بالضرورة استخدام محور الاسناد sʹ او ما يسمى بمحاور مركز الكتلة لكي نتجنب بعض العلاقات المعقدة.
اولا : نطبق الان قانون حفظ الزخم فيكون :
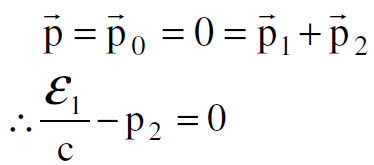
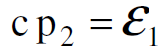 (1.3)
(1.3)
ثانيا : ونطبق قانون حفظ الطاقة فنحصل على :
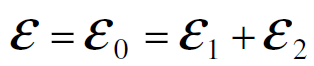
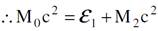 (1.4)
(1.4)
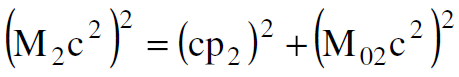 (1.5)
(1.5)
ومن (1.3) و (1.5) نجد أن :
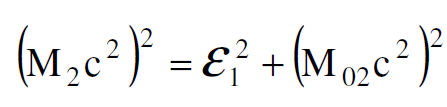 (1.6)
(1.6)
ومن العلاقة (1.4) و (1.6) نحصل على :
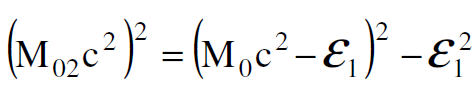
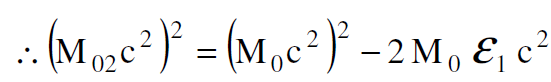 (1.7)
(1.7)
الان M02c2, M0c2 هما طاقتا السكون للذرة في الحالة الابتدائية والنهائية ولنهما قيمة محدودة وان الفرق بينهما يساوي طاقة ثابتة :
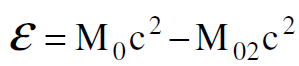 (1.8)
(1.8)
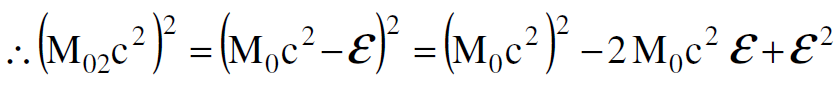 (1.9)
(1.9)
وبمقارنة العلاقتين (1.7)و (1.9) ينتج ان :
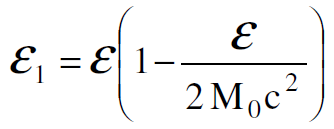 (1.10)
(1.10)
ولكون طاقة الفوتون تتناسب مع التردد فان التردد يقل ويزداد الطول الموجي إلا في حالة واحدة وهي اذا امكن تثبيت الذرة ومنعها من الارتداد كي تعطي الطاقة المتحررة ε بأجمعها الى الفوتون المتحرر خلال عملية الانبعاث.
ان هذه النتائج لها اعتبارات فيزيائية مهمة لأنها تبين حدود إمكانية النوى والذرات بان تقوم مرة اخرى بامتصاص او طرد (انبعاث) الاشعاع الخاص بها. إن اي عنصر عندما يصبح في حالة استعداد للإشعاع كأنبوبه التفريغ الكهربائي مثلا، فانه يقوم بإشعاع (انبعاث) الطيف الخطي الخاص به، كما في سلسلة بالمر للهيدروجين. إن هذه الخطوط الطيفية تكون حادة بحيث ان كل خط يمثل اطوالا موجبة ضمن مدى ضيق جدا. ان ضيق هذه الخطوط هو تعبير عن حقيقة ان الذرات نفسها لا تستطيع ان تتواجد في مستويات طاقة عشوائية، اي غير محددة (اعتباطية) ولكنها مرتبطة بسلسلة ضيقة من هذه المستويات. ان انبعاث فوتون من الذرة عندما تنتقل من المستوى f الى المستوى < f ) ii) يقابله نقصان معين في الطاقة ( او الكتلة) للذرة كما تصفه العلاقة (1.8). فاذا صادف هذا الفوتون المنبعث والذي يحمل طاقة مقدارها hv، ذرة اخرى مماثلة تقع في المستوى i وهي في حالة سكون فلن تكون هذه الطاقة كافية لرفع تلك الذرة الى المستوى f لان جزءا صغيرا من طاقة الفوتون قد صرف على طاقة ارتداد الذرة، لذلك ينبغي ان يؤخذ بعين الاعتبار التأثير الارتدادي للذرة خلال عمليات الانبعاث والامتصاص كما بالشكل (1.3). لقد قام العالم موسباور بدراسة التأثير الارتدادي للذرات والنوى خلال عمليات الامتصاص والانبعاث الرنيني، حيث تمكن من التغلب على طاقة الارتداد للنوى باستخدام مصدر مشع متحرك، وتسمى هذه الظاهرة موسباور
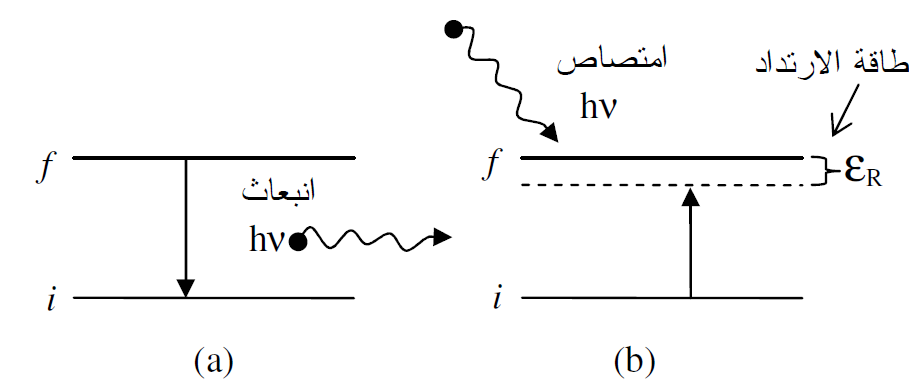
الشكل (1.3) : يوضح عملية الانبعاث (a) و الامتصاص (b) في الذرات.
فمن قانون حفظ الزخم الكلي قبل الانبعاث وبعد الانبعاث :
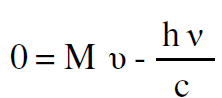 (1.11)
(1.11)
حيث ان الصفر في الجزء الايسر للمعادلة يدل على ان الذرة ساكنة قبل عملية الانبعاث اما Mv في الجزء الايمن من المعادلة فهو زخم الذرة المرتدة و 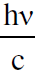 زخم الفوتون المنبعث كما بالشكل (1.4).
زخم الفوتون المنبعث كما بالشكل (1.4).
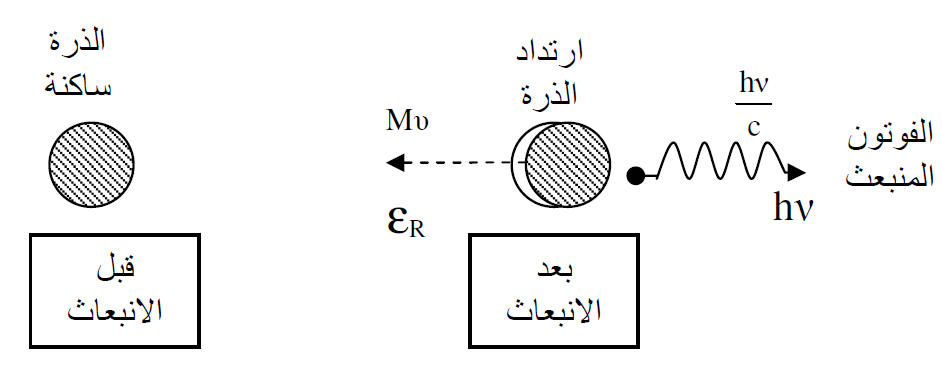
الشكل (1.4) : يوضح عملية الارتداد الناتجة عن انبعاث فوتون من الذرة.
من المعادلة الاخيرة نجد ان سرعة ارتداد الذرة تساوي :
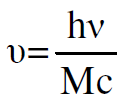
وبما أن طاقة الارتداد Rε تساوي الطاقة الحركية للذرة، اذن من سرعة ارتداد الذرة يمكننا حساب طاقة الارتداد كما يلي :
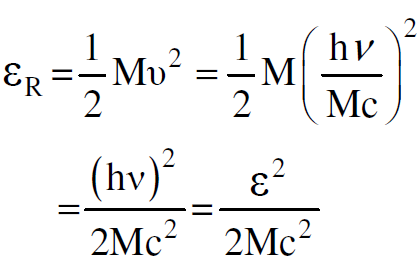
اذا نستنتج انه اذا كانت مستويات الطاقة ضيقة بصورة تامة واذا كانت الذرات التي تولد الاشعاع او تمتصه في حالة سكون فان هذه الذرات تكون شفافة للإشعاع الذي ينبعث منها بغض النظر عن التأثيرات الجانبية التي تغير الحالة التي وصفت كالحركة الناتجة عن الاثارة الحرارية التي تبطل التأثيرات الارتدادية للذرات خلال عمليات الانبعاث او الامتصاص.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
مؤتمر ذاكرة الألم يشهد عرضًا بتقنية الواقع الافتراضي يُجسّد مأساة الأيزيديين
|
|
|