


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
أقرأ أيضاً
التاريخ: 10-8-2016
التاريخ: 22-8-2016
التاريخ: 17-9-2016
التاريخ: 3-9-2016
|
ابن الحاسب الكرخي
ابو بكر محمد بن الحساب الكرخي، ويسمى في بعض المصادر الكرجي، ولكن المؤرخين متفقون على تلقيبه بالكرخي نسبة الى كرخ وهي ضاحية من ضواحي بغداد وفيها ولد، كعادة المؤرخين فانهم لم يذكروا تاريخ ولادته وان كانوا قد ارخا لوفاته في بغداد سنة 421 هـ كان من اشهر علماء بغداد في علوم الرياضيات، الف كتابا في الحساب لم يستعمل في الارقام بل اعتمد الاعداد تكتب كاملة بالحروف.
امضى ابن الحاسب شرطا كبيرا من عمره في المناطق الجبلية حيث عمل بالهندسة، وهذا ما يتضح من كتابه المعنون حول حفر الابار قال عنه عمر رضا كحالة في العلوم البحتة : ان الكرخي من اعظم نوابغ الرياضيين الذين ظهروا في بداية القرن الخامس الهجري، والذين كان لهم اثر حقيقي في تقدم العلوم الرياضية.
وقد اهتم الكرخي اهتماما بالغ بعلم الحساب والجبر ايضا، فكان نتاجه عظيما في هذين العلمي حيث بقيت اوروبا تنهل منها حقبة طويلة من الزمن، يقول المؤرخ جورج سارتون في تاريخ العلوم الانسانية : ان اوروبا مدينة للكرخي الذي قدم للرياضيات اهم واكمل نظرية : في علم الجبر عرفتها، كما بقيت حتى القرن التاسع عشر تعتمد مصنفاته في الحساب والجبر، وقد ترجم هوسيلم كتاب الكافي في الحساب ابن الألمانية، فكان لهذا الكتاب اثره في العماء آنذاك وبقي مرجعا لديهم الى زمن قريب.
يقول الكرخي في مقدمة الكافي : اني وجدت علم الحساب موضوعاً لإخراج المجهولات من المعلومات في جميع انواعه، والفيت اوضح الابواب اليه، واول الاسباب عليه، صناعة الجبر والمقابلة، لقوتها واطرادها في جميع المسائل الحسابية على اختلافها، ورأيت الكتب المصنفة فيها غير ضامنة لها يحتاج اليه من معرفة اصولها، ولا وافية بما يستعان به على علم فروعها، وان مصنفيها اهملوا شرح مقدمتها التي هي السبيل الى الغاية والموصلة الى النهاية، ثم لم اجد في كتبهم لها ذكراً ولا بيانا فلما ظفرت بهذه الفضيلة واحتجت الى جبر تلك النقيصة لم اجد ابدا من تأليف كتاب يحيط بها ويشتمل عليها، الخص فيه شرح اصولها، مصفى من كدر الحشو ودر اللغو.
كان الكرخي شديد الولع بعلمي الحساب والجبر كما هو كذلك لم يترك موضوعا فيها الا طرقه وطور فيه، وكان من العلماء والمبرزين المبتكرين الذين يفضلون التاليف والتعليق والشرح والتعليق على مصنفات المتقدمين، وقد قام لأجل هذا بشرح وتوضيح الكثير من النقط الغامضة في كتاب الجبر والمقابلة لمحمد بن موسى الخوارزمي واكدها بأمثلة من عنده كثيرة، يقول الاستاذ روس بول في ملخص تاريخ الرياضيات : ان الكرخي طور قانون مجموع مربعات الاعداد الطبيعية الى درجة لم يسبقه اليها احد، ولا تزال في القرن العشرين تستعمل دون أي تغيير يذكر واضاف الدكتور فلورين كاجوري في كتابه تاريخ الرياضيات : ان الكرخي يجب ان يعتبر مبتكرا لنظرية مجموع الاعداد الطبيعية.
لقد جهد الكرخي في التأليف فترك لنا عددا وفيرا من المؤلفات التي امتازت بالابتكار منها :
كتاب الفخري في الحساب (وضعه بين 401 و 407 هـ) قيل عنه ان هذا الكتاب في الحساب احسن كتاب كتب في علم الجبر في العصور الوسطى، مستندا على كتاب محمد بن موسى الخوارزمي الجبر والمقابلة وامتاز هذا الكتاب ايضا بطابعه الاصيل في علم الجبر لما فيه من الابتكارات الجديدة والمسائل التي لا يزال لها دور في الرياضيات الحديثة، وقد اكد ديفيد سميث في كتابه تاريخ الرياضيات ان كتاب الفخري في الحساب له الاثر الكبير في علم الجبر، ويمكن اعتباره مقياسا صحيحا لما وصل اليه العرب والمسلمون من التقدم في هذا الفرع.
رسالة فيها مساحات بعض السطوح.
ابتكارات الكرخي في مؤلفاته الرياضية :
بالنسبة الى النظريات التي تتعلق بإيجاد مجموع مربعات ومكعبات الاعداد التي عددها ن :
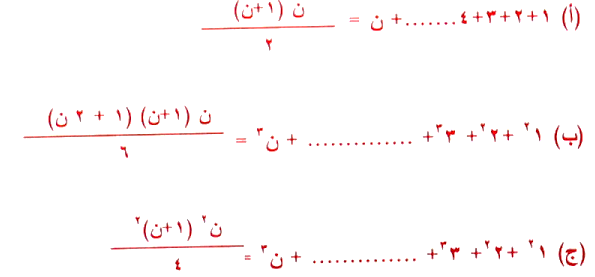
عددان مجموع مكعبيهما يساوي مربع العدد الثالث أي س3 + ص3 = ع2
في هذه المسالة جاء الكرخي باستعمال الاعداد الجذرية.
ففرض ان ص = م س، ع = ن س

بقسمة الطرفين على س2 ← س (1+م3) = ن2
لهذا تكون حيث ان كلا من م، ن عددان جذريان اختياريان.
اختار الكرخي حالة خاصة حيث اعتبر ان س = 1، ص = 2، ع = 3.
لذلك يكون الناتج 1 3 + 2 3 + 3 2
من هنا استنتج الكرخي ان : أس ن + ص ن = م ع ن - 1
وهي معادلة يكاد لا يخلو منها أي مؤلف في علم الجبر.



|
|
|
|
لشعر لامع وكثيف وصحي.. وصفة تكشف "سرا آسيويا" قديما
|
|
|
|
|
|
|
كيفية الحفاظ على فرامل السيارة لضمان الأمان المثالي
|
|
|
|
|
|
|
العتبة العباسية المقدسة تجري القرعة الخاصة بأداء مناسك الحج لمنتسبيها
|
|
|