Two spaceships, A and B, move toward one another on courses for a head-on collision. According to an observer at rest in an inertial reference frame, both have speed V along the x-axis. At the time of observation, spaceship A is coincident with the observer that is, has the same x value. Spaceship B is at a distance L away. One would like to know how much later the collision occurs according to the observer and according to an observer aboard spaceship A.

Let us propose a solution method. According to the observer, the collision occurs when spaceship A or B travels L/2, half the distance between them, which requires the elapsed time T = L/2V. Put into a better format, three events occur:

Event 1:          X₁ = 0         T₁ = 0

Event 2:         X₂ = L          T₂ = 0

Event 3:         X₃ = L/2       T₃ = L/2V

These same events can be specified in the inertial (primed) frame of spaceship A as:

Event 1′:           X₁′ = 0         T₁′ = 0

Event 2′:          X₂′ = ?           T₂′ = ?

Event 3′:          X₃′ = ?          T₃′ = ?

Answer

The method of determining position and clock reading for the three events first before answering the question is a good one. However, the values inserted already are not all correct for the observer. Simultaneous measurements at both the origin X₁ = 0 and at X₂ = L cannot be made by the method assumed since they are not equidistant. Therefore, if the notation (X, T) is correctly (0, 0) for event 1, then event 2 is labeled by (L, –L/c) because the light from event 2 takes L/c seconds to travel the distance L to the observer. Event 3 is not at position L/2 between the two spaceships at T = 0 because spaceship B has already traveled for L/c seconds. Therefore the distance between the two spaceships is L – VL/c. Thus T₃ = L(1 – V/c)/2V. We can summarize the events as:

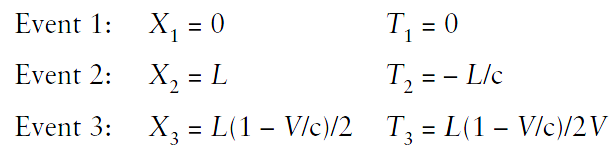
These same events can be specified in the inertial frame (primed) of spaceship A as:

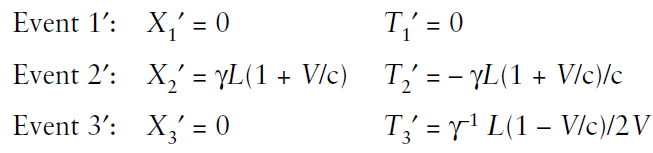
We have defined 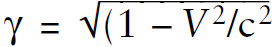 and have used the normal Lorentz transformations x′ = γ (x – Vt) and t′ = γ (t – Vx/c²) of the STR.

Now, finally, we can determine the clock reading that is, the elapsed time for the observer who sees the collision a distance L(1 – V/c)/2 away as T = L(1 – V/c)/2V + L(1 – V/c)/2, which reduces to T = L(1 – V²/c²)/2V. The observer on spaceship A has an elapsed time of γ^–1 L(1 – V/c)/2V.