Photon Engine

The ideal Carnot heat engine converts heat to work without the engine itself being a source of any work. The reversible closed Carnot cycle consists of two isothermal (constant temperature) processes and two adiabatic (no external exchange of thermal energy) processes. No heat engine operating between two temperatures can be more efficient than a Carnot cycle.

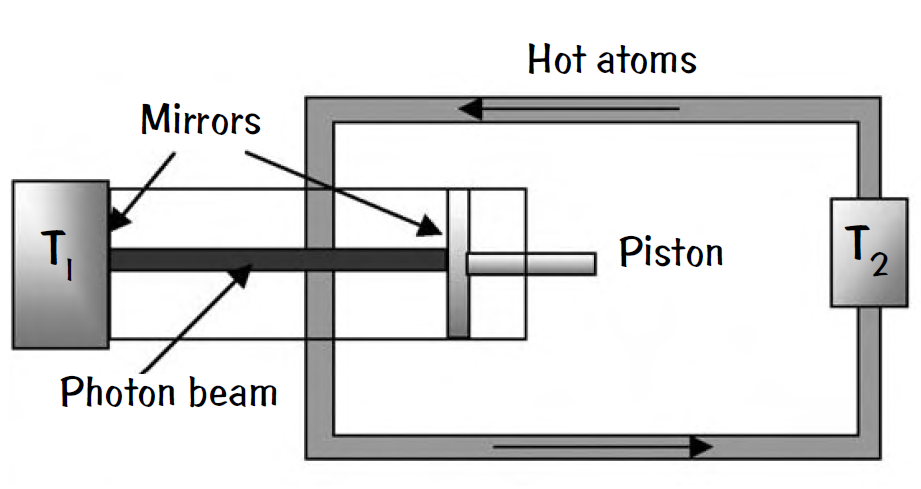
But Carnot could be wrong. The challenger is the new “quantum Carnot engine,” in which the radiation pressure from photons drives a piston in an optical cavity. The inward-facing surface of the piston is mirrored and the other cavity mirror is fixed in place while exchanging thermal energy with a heat sink at temperature T₁. A second heat bath at a higher temperature, T₂, provides the source of thermal energy for the photons.

This source of thermal energy is a stream of hot atoms, which flows into the optical cavity and exchanges thermal energy with the photons through emission and absorption processes. These atoms exit the cavity at a cooler temperature and are reheated to T₂ in a second cavity, to be reinjected into the first cavity for the next cycle of the quantum Carnot engine.

Therefore, the quantum and classical Carnot engines operate in the same way as a closed cycle of two isothermal and two adiabatic processes. However, in its simplest form, when each bath atom is treated as a two-state system, the quantum Carnot engine cannot extract work from a single heat bath. Why not? Will the engine work if each bath atom is a three-state system?

Answer

We can analyze the operation of the quantum Carnot engine in the same manner in which we would analyze a classical Carnot engine. Let Q_in be the energy absorbed from the bath atoms during the isothermal expansion and Q_out be the energy given to the heat sink during the isothermal compression. Then the Carnot engine efficiency η = (Q_in – Q_out)/Q_in.

If the bath atoms are assumed to be two-state systems that absorb and emit radiation at the same photon frequency, then we need the thermodynamic properties of a photon gas in order to determine the theoretical efficiency of this photon engine. Assuming thermal equilibrium for the photon gas, the average number of photons n₂ with energy ε coming in from the heat bath at temperature T₂ is given by n₂ = 1/(exp[ε/kT₂] – 1), while the average number of photons n₁ leaving at temperature T₁ is n₁ = 1/(exp[ε/kT₁] – 1). Since Q_in ∝ n₂ ε and Q_out ∝ n₁ ε, the efficiency of the quantum Carnot engine is η = 1 – T₁/T₂, exactly the same as for the classical Carnot engine. When there is only one heat bath, with T₁ = T₂, no work can be done.

A different quantum engine occurs when the bath atoms have three states instead of two, bringing in quantum behavior called quantum coherence, with a non-vanishing phase difference between the two lowest atomic states induced by a microwave field. One can eliminate the photon absorption process (analogous to laser operation without a population inversion). The temperature T₂ becomes altered to a different effective temperature, T_φ. The efficiency η_φ = (T_φ – T₁)/T₁ can exceed the efficiency of the classical Carnot engine. This quantum engine can extract work from a single heat bath, even when T₁ = T₂! For the details of the three-state quantum engine’s operation, see the reference below.