Bragg Scattering of X-rays

Bragg scattering of X-rays of wavelength λ in an ideal crystal satisfies Bragg’s law: 2d sin θ = m λ, where d is the spacing between adjacent scattering planes and θ is the angle measured from the surface of the crystal, not the perpendicular. When this condition is met for various integer values of m, constructive interference from the entire family of parallel planes occurs because the path differences are integral multiples of the X-ray wavelength. One often reads that the Bragg scattering of X-rays from an ideal crystal is a coherent scattering process that is, all the Bragg-scattered X-rays arrive in phase at the detector. Why is it not so?

Answer

Bragg scattering requires λ < d; therefore there will not be any collective scattering from a group of scatterers at different atoms within one wavelength. The actual scatterers of the X-rays are the electrons at each atom in these planes of the crystal. Coherent scattering requires fixed phase relationships, but there is no fixed phase relationship between electrons at different atoms nor between the electrons doing the scattering at any moment. Therefore, the X-rays scattered into the Bragg angle have a multitude of random phases and not fixed-phase relationships. The scattering probability is proportional to N, the number of scatterers, and not N² , as it would be for coherent scattering.

Here is the QM argument mathematically. Let ψ_i represent the probability amplitude to scatter an X-ray at the i th atom. We know from QM rule 2 that Ψ = ψ₁ + ψ₂ + ψ₃ + . . . , for alternative ways to go from the X-ray source to the crystal to the X-ray detector. Each ψ_i represents one atom, and we assume single scatterings on the way to the detector for simplicity. Each ψ_i = exp[iδ] φ_i , which includes a phase part exp[iδ] and the identical scattering amplitude φ_i at the identical atoms in the crystal. If the phase part at each scattering atom is identical, then we would have Ψ = N ψ₁ and the probability P = N² |ψ₁| ², giving us coherent scattering proportional to N².

However, there is no correlated motion between electrons on different atoms, so their phases are random. If the phase differences between scatterers that is, the electrons on different atoms are not fixed differences, then the sum is over random phases and, like the random walk problem, the total amount is proportional to 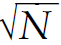 instead of N. Therefore Ψ =  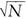ψ₁, so P = N |ψ₁|². The Bragg scattering of X-rays is not a coherent scattering process.