
Interpretation of entropy
 المؤلف:
Heino Falcke and Friedrich W Hehl
المؤلف:
Heino Falcke and Friedrich W Hehl
 المصدر:
THE GALACTIC BLACK HOLE Lectures on General Relativity and Astrophysics
المصدر:
THE GALACTIC BLACK HOLE Lectures on General Relativity and Astrophysics
 الجزء والصفحة:
p 218
الجزء والصفحة:
p 218
 26-1-2017
26-1-2017
 1647
1647
Interpretation of entropy
We have seen in the previous section that if quantum theory is taken into account black holes emit thermal radiation. Consequently, the laws of black hole mechanics discussed indeed, have a physical interpretation as thermodynamical laws black holes are thermodynamical systems.
One can therefore also infer an expression for the black hole entropy. From dM = TBH dSBH one finds the ‘Bekenstein–Hawking entropy’:
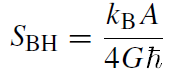 (1.1)
(1.1)
in which the unknown factor has now been fixed. For the special case of a Schwarzschild black hole, this yields
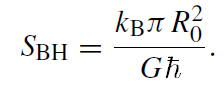 (1.2)
(1.2)
It can easily be estimated that SBH is much bigger than the entropy of the star that collapsed to form the black hole. The entropy of the sun, for example, is Sּ ≈ 1057kB, whereas the entropy of a solar-mass black hole is about 1077kB, which is 20 orders of magnitude larger! For the Galactic black hole, the entropy is SGBH ≈ 1090kB which is 100 times the entropy of the Universe. (Under the ‘entropy of the Universe’ I understand the entropy of the present Universe up to the Hubble radius without taking black holes into account. It is dominated by the entropy of the cosmic microwave background radiation.)
Can a physical interpretation of this huge discrepancy be given? Up to now, the laws of black hole mechanics are only phenomenological thermodynamical laws. The central open question therefore is: can SBH be derived from quantum statistical considerations? This would mean that SBH could be calculated from a Gibbs type formula according to
 (1.3)
(1.3)
where ρ denotes an appropriate density matrix and SSM is the quantum statistical entropy; SBH would then somehow correspond to the number of quantum microstates that are consistent with the macro state of the black hole that is according to the no hair theorem uniquely characterized by mass, angular momentum, and charge. Some important questions are:
● Does SBH correspond to states hidden behind the horizon?
● Or does SBH correspond to the number of possible initial states?
● What are the microscopic degrees of freedom?
● Where are they located (if at all)?
● Can one understand the universality of the result?
● What happens to SBH after the black hole has evaporated?
● Is the entropy a ‘one-loop’ or a ‘tree-level’ effect?
The attempts to calculate SBH by state counting are usually done in the ‘one loop limit’ of quantum field theory in curved spacetime this is the limit where gravity is classical but non-gravitational fields are fully quantum, and it is the limit where the Hawking has been derived. The expression (1.1) can already be calculated from the so called ‘tree level’ of the theory, where only the gravitational degrees of freedom are taken into account. Usually a saddle point approximation for a Euclidean path integral is being performed. Such derivations are, however, equivalent to derivations within classical thermodynamics, cf Wald (2001).
If the entropy (1.1) is to make sense, there should be a generalized Second Law of Thermodynamics according to which
 (1.4)
(1.4)
where SM denotes the non-gravitational entropy. The validity of (1.4), although far from being proven in general, has been shown in a variety of thought experiments. One of the most instructive of these was devised by Unruh and Wald. It makes use of the box that is adiabatically lowered towards a (spherically symmetric) black hole.
At asymptotic infinity r → ∞, the black hole radiation. However, for finite r , the temperature is modified by the occurrence of a redshift factor χ(r) ≡ (1 − 2GM/r )1/2 in the denominator. Since the box is not in free fall, it is accelerated with an acceleration a. From the relation (Wald 1984)
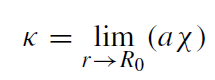 (1.5)
(1.5)
one has
 (1.6)
(1.6)
which is just the Unruh temperature! This means that a freely falling observer near the horizon observes no radiation at all, and the whole effect (1.6) comes from the observer (or box) being non-inertial with acceleration a.
The analysis of Unruh and Wald, which is a generalization of the thought experiment, shows that the entropy of the black hole increases at least by the entropy of the Unruh radiation displaced at the floating point this is the point where the gravitational force (pointing downwards) and the buoyancy force from the Unruh radiation (1.6) are in equilibrium. Interestingly, it is just the application of ‘Archimedes’ principle’ to this situation that rescues the generalized Second Law (1.4).
An inertial, i.e. freely falling, observer does not see any Unruh radiation. How does he/she interpret this result? For him/her the box is accelerated and therefore the interior of the box fills up with negative energy and pressure a typical quantum effect that occurs if a ‘mirror’ is accelerated through the vacuum. The ‘floating point’ is then reached after this negative energy is so large that the total energy of the box is zero.
I want to conclude this section with some speculations about the final stages of black hole evolution and the information loss problem. The point is that in the semiclassical approximation used by Hawking the radiation of a black hole seems to be purely thermal. If the black hole evaporates completely and leaves only thermal radiation behind, one would have a conflict with established principles in quantum theory: any initial state (in particular a pure state) would evolve into a mixed state. In ordinary quantum theory, because of the unitary evolution of the total system, this cannot happen. Formally, Tr ρ2 remains constant under the von Neumann equation; the same is true for the entropy SSM = −kB Tr(ρ ln ρ): For a unitarily evolving system, there is no increase in entropy. If these laws were violated during black hole evaporation, information would be destroyed. This is, indeed, the speculation that Hawking made after his discovery of black hole radiation. The attitudes towards this information-loss problem can be roughly divided into the following classes:
● The information is indeed lost during black hole evaporation, and the quantum mechanical Liouville equation is replaced by an equation of the form
 (1.7)
(1.7)
where $ is Hawking's dollar matrix which generalizes the ordinary S-matrix S.
● The full evolution is in fact unitary; the black hole radiation contains subtle quantum correlations that cannot be seen in the semiclassical approximation.
● The black hole does not evaporate completely, but leaves a ‘remnant’ with mass in the order of the Planck mass that carries the whole information.
In my opinion, the information-loss problem is only a pseudo problem. Already in the original calculation of Hawking (1975) only pure states appear. Reference to thermal radiation is being made because the particle number operator in the final pure state possesses an exact Planckian distribution. As has been shown in Kiefer (2001), the coupling of this pure state (a squeezed state in quantum-optics language) to its natural environment produces a thermal ensemble for the Hawking radiation, which constitutes an open quantum system, after this environment has been traced out. The thermal nature of this radiation is thus a consequence of decoherence (Giulini et al 1996).
There exist many attempts to derive the Bekenstein–Hawking entropy (1.1) within approaches to quantum gravity, see, e.g., Kiefer (1999) and Wald (2001) for more details and references. Examples are the derivations within superstring theory (counting of states referring to microscopic objects called D-branes), canonical quantum gravity, Sakharov's induced gravity, conformal field theories, and others. Although many of these look very promising, a final consensus has not yet been reached.
 الاكثر قراءة في الثقوب السوداء
الاكثر قراءة في الثقوب السوداء
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


