
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
The laws of black hole mechanics
المؤلف:
Heino Falcke and Friedrich W Hehl
المصدر:
THE GALACTIC BLACK HOLE Lectures on General Relativity and Astrophysics
الجزء والصفحة:
p 208
26-1-2017
3562
The laws of black hole mechanics
It is a most amazing fact that black holes obey uniqueness theorems (Heusler 1996). If an object collapses to form a black hole, a stationary state is reached asymptotically. One can prove within Einstein–Maxwell theory that stationary black holes are uniquely characterized by only three parameters: mass M, angular momentum J ≡ Ma, and electric charge q. In this sense, black holes are objects much simpler than ordinary stars given these parameters, they all look the same. All other degrees of freedom that might have been initially present have thus been radiated away, e.g. in the form of electromagnetic or gravitational radiation, during the collapse. Since the latter constitute some form of ‘hair’, one refers to the content of these theorems as black holes have no hair. The three parameters are associated with conservation laws at spatial infinity. In principle, one can thus decide about the nature of a black hole far away from the hole itself, without having to approach it. In astrophysical situations, the two parameters M and J suffice, since a charged object would rapidly discharge. The corresponding solution of Einstein's equations is called the Kerr solution (Kerr-Newman in the presence of charge). Stationary black holes are axially symmetric, with spherical symmetry being obtained as a special case for J = 0.
In the presence of other fields, the uniqueness theorems do not always hold, see, for example, Nunez et al (1998). This is, in particular, the case in the presence of non-Abelian gauge fields. In addition to charges at infinity, such ‘coloured black holes’ have to be characterized by additional variables, and it is necessary to approach the hole to determine them. The physical reason for the occurrence of such solutions is the nonlinear character of these gauge fields. Fields in regions closer to the black hole (that would otherwise be swallowed by the hole) are tied to fields far away from the hole (that would otherwise be radiated away) to reach an equilibrium situation. In most examples this equilibrium is, however, unstable and the corresponding black hole solution does not represent a physical solution. Since classical non-Abelian fields have never been observed (the description of objects such as quarks necessarily needs quantized gauge fields which, due to confinement, have no macroscopic limits), they will not be taken into account in the subsequent discussion.
In 1971, Stephen Hawking could prove an important theorem about stationary black holes that their area can never decrease with time. More precisely, he showed that for a predictable black hole satisfying Rabkakb ≥ 0 for all null ka, the surface area of the future event horizon never decreases with time.
A ‘predictable’ black hole is one for which the cosmic censorship hypothesis holds this is thus a major assumption for the area law. Cosmic censorship states that all black holes occurring in nature have an event horizon, so that the singularity cannot be observed for far-away observers (the singularity is not ‘naked’). I emphasize that the time asymmetry in this theorem comes into play because a statement is made about the future horizon, not the past horizon; an analogous statement for white holes would then be that the past event horizon never increases. I also emphasize that the area law only holds in classical theory, not in quantum theory.
The area law seems to exhibit a close formal analogy to the Second Law of Thermodynamics there the entropy can never decrease with time (for a closed system). However, the conceptual difference could not be more pronounced: while the Second Law is related to statistical behaviour, the area law is just a theorem in differential geometry. That the area law is in fact directly related to the Second Law will become clear in the course of this section. Further support for this analogy is given by the existence of analogies to the other laws of thermodynamics. The Zeroth Law states that there is a quantity, the temperature, that is constant on a body in thermal equilibrium. Does there exist an analogous quantity for a black hole? One can in fact prove that the surface gravity κ is constant over the event horizon (Wald 1984). For a Kerr black hole, κ is given by
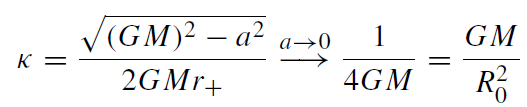 (1.1)
(1.1)
where r+ denotes the location of the event horizon. One recognizes in the Schwarzschild limit the well-known expression for the Newtonian gravitational acceleration. (There R0 ≡ 2GM denotes the Schwarzschild radius.) One can show for a static black hole that κ is the limiting force that must be exerted at infinity to hold a unit test mass in place when approaching the horizon. This justifies the name surface gravity.
With a tentative formal relation between surface gravity and temperature, and between area and entropy, the question arises as to whether a First Law of thermodynamics can be proved. This can in fact be done and the result for a Kerr-Newman black hole is
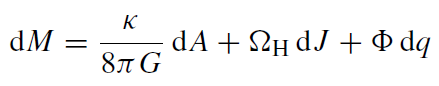 (1.2)
(1.2)
where A,ΩH, denote the area of the event horizon, the angular velocity of the black hole, and the electrostatic potential, respectively. This relation can be obtained by conceptually different methods: a physical process version in which a stationary black hole is altered by infinitesimal physical processes, and an equilibrium state version in which the areas of two stationary black hole solutions to Einstein's equations are compared. Both methods lead to the same result (1.2).
Since M is the energy of the black hole, (1.2) is the analogue of the First Law of Thermodynamics given by
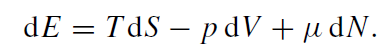 (1.3)
(1.3)
Table 1.1. Analogy between the laws of thermodynamics and the laws of black-hole mechanics.

‘Modern’ derivations of (1.2) make use of both Hamiltonian and Lagrangian methods of general relativity. For example, the First Law follows from an arbitrary diffeomorphism invariant theory of gravity whose field equations can be derived from a Lagrangian.
What about the Third Law of Thermodynamics? A ‘physical process version’ was proved by Israel it is impossible to reach κ = 0 in a finite number of steps, although it is unclear whether this is true under all circumstances (Farrugia and Hajicek 1979). This corresponds to the ‘Nernst version’ of the Third Law. The stronger ‘Planck version’, which states that the entropy goes to zero (or a material-dependent constant) if the temperature approaches zero, does not seem to hold. The analogies are summarized in table 1.1.
The identification of the horizon area with the entropy for a black hole can be obtained from a conceptually different point of view. If a box with, say, thermal radiation of entropy S is thrown into the black hole, it seems as if the Second Law could be violated, since the black hole is characterized only by mass, angular momentum, and charge, but nothing else. The demonstration that the Second Law is fulfilled leads immediately to the concept of a black hole entropy, as will now be discussed (Bekenstein 1980, Sexl and Urbantke 1983).
Consider a box with thermal radiation of mass m and temperature T lowered from a spaceship far away from a spherically symmetric black hole towards the hole (figure 1.1). As an idealization, both the rope and the walls are assumed to have negligible mass. At a coordinate distance r from the black hole, the energy of the box is given by
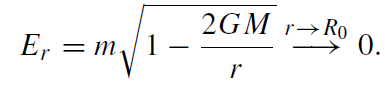 (1.4)
(1.4)
If the box is lowered down to the horizon, the energy gain is thus given by m. The box is then opened and thermal radiation of mass δm escapes into the hole. If the box is then closed and brought back again to the spaceship, the energy loss is m − δm. In total the energy δm of the thermal radiation can be transformed into work with an efficiency of η = 1 . This looks as if one possessed a perpetuum mobile of the second kind.

Figure 1.1. Thought experiment to demonstrate the Second Law of Thermodynamics for black holes.
The key to the resolution of this apparent paradox lies in the observation that the box must be big enough to contain the wavelength of the enclosed radiation. This, in turn, leads to a lower limit on the distance to which the box can approach the horizon. Therefore, only part of δm can be transformed into work, as I shall show now.
According to Wien's law, one must have a linear extension of the box of at least
 (1.5)
(1.5)
where kB denotes Boltzmann's constant. I emphasize at this stage that Planck's constant h comes into play. The box can then be lowered down to the coordinate distance δr (assumed to be << 2GM) from the black hole where, according to the Schwarzschild metric, the relation between δr and λmax is
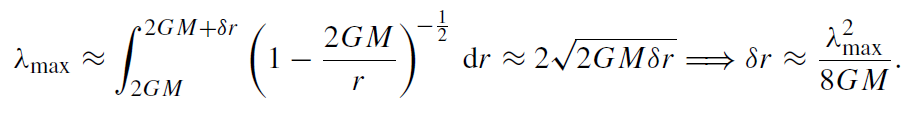
According to (1.4), the energy of the box at r = 2GM + δr is

Recalling that, according to (1.2), the formal temperature of the black hole, TBH, is proportional to the surface gravity κ = 1/(4GM), the energy of the box before opening is

while after opening it is
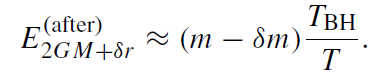
The efficiency of transforming thermal radiation into work is thus given by
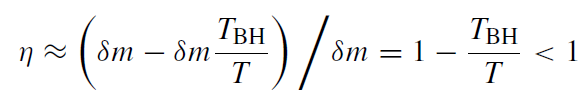
which is the well-known Carnot limit for the efficiency of heat engines. From the First Law (1.2) one then finds for the entropy of the black hole SBH ∝ A = 16π(GM)2. It is this agreement of conceptually different approaches to black hole thermodynamics that gives us confidence in the physical meaning of these concepts. In the next section I shall show how all these formal results can be physically interpreted in the context of quantum theory.
 الاكثر قراءة في الثقوب السوداء
الاكثر قراءة في الثقوب السوداء
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















