
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
The 3 + 1 split and the Cauchy initial value problem
المؤلف:
Heino Falcke and Friedrich W Hehl
المصدر:
THE GALACTIC BLACK HOLE Lectures on General Relativity and Astrophysics
الجزء والصفحة:
p 186
29-1-2017
1613
The 3 + 1 split and the Cauchy initial value problem
We saw that the ten Einstein equations decompose into two sets of four and six equations respectively, four constraints which the initial data have to satisfy, and six equations driving the evolution. As a consequence, there will be four dynamically undetermined components among the ten components of the gravitational field gμν. The task is to parametrize the gμν in such a way that four dynamically undetermined functions can be cleanly separated from the other six. One way to achieve this is via the splitting of spacetime into space and time. The four dynamically undetermined quantities will be the famous lapse (one function α) and shift (three functions βi ). The dynamically determined quantity is the Riemannian metric hi j on the spatial three manifolds of constant time. These together parametrize gμν as follows:
 (1.1)
(1.1)
The physical interpretation of α and βi is: think of spacetime as the history of space. Each ‘moment’ of time, x0 = t, corresponds to an entire three-dimensional slice Σt . Obviously there is plenty of freedom in how to ‘waft’ space through spacetime. This freedom corresponds precisely to the freedom to choose the 1+3 functions α and βi . For one thing, you may freely specify how far for each parameter step dt you push space in a perpendicular direction forward in time. This is controlled by α, which is just the ratio ds/dt of the proper perpendicular distance between the hypersurfaces Σt and Σt+dt . This speed may be chosen in a space and time-dependent fashion, which makes α a function on spacetime. Second, let a point be given with coordinates xi on Σt . Going from xi in a perpendicular direction you meet Σt+dt in a point with coordinates xi + dxi , where dxi can be chosen at will. This freedom of moving the coordinate system around while evolving is captured by βi ; one writes dxi = βidt. Clearly this moving around of the spatial coordinates can also be made in a space- and time dependent fashion, so that the βi are functions of spacetime, too.
Let nμ be the vector field in a spacetime which is normal to the spatial sections of constant time. It is given by n = 1/α (∂/∂x0 − βi∂/∂xi ), as one may readily verify by using (1.1) (you have to check that n is normalized and satisfies g(n, ∂/∂xi ) = 0). We define the extrinsic curvature, Ki j , to be one half the Lie derivative of the spatial metric in the direction of the normal:
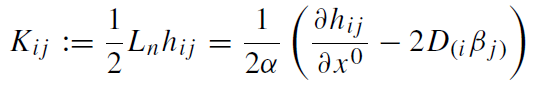 (1.2)
(1.2)
where D is the spatial covariant derivative with respect to the metric hi j. As usual, a round bracket around indices denotes their symmetrization. Note that, by definition, Ki j is symmetric. Finally we denote the Ricci scalar of hi j by R(3). We can now write down the four constraints of the vacuum Einstein equations in terms of these variables:
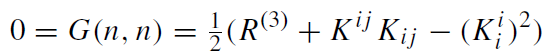 (1.3)
(1.3)
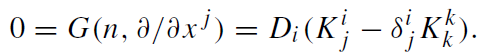 (1.4)
(1.4)
Equations (1.3) and (1.4) are referred to as the Hamiltonian constraint and momentum constraint, respectively. The six evolution equations of second order in the time derivative can now be written as 12 equations of first order. Six of them are just (1.2), read as the equation that relates the time derivative ∂hi j /∂x0 to the ‘canonical data’ (hi j , Ki j ). The other six equations, whose explicit form needs not concern us here, express the time derivative of Ki j in terms of the canonical data. Both sets of evolution equations contain, on their right-hand sides, the lapse and shift functions, whose evolution is not determined but must be specified by hand. This specification is a choice of gauge, without which one cannot determine the evolution of the physical variables (hi j , Ki j ).
The initial data problem takes now the following form:
(1) Choose a topological three manifold Σ.
(2) Find on Σ a Riemannian metric hi j and a symmetric tensor field Ki j which satisfy the constraints (1.3) and (1.4).
(3) Choose a lapse function α and a shift vector field βi , both as functions of space and time, possibly according to some convenient prescription (e.g. singularity avoiding gauges, like maximal slicing).
(4) Evolve initial data with these choices of α and βi according to the 12 equations of first order. By consistency of Einstein’s equations, the constraints will be preserved during this evolution, independent of the choices for α and βi .
The backbone of this setup is a mathematical theorem, which states that for any set of initial data, taken from a suitable function space, there is, up to a diffeomorphism, a unique maximal Einstein spacetime developing.
 الاكثر قراءة في الثقوب السوداء
الاكثر قراءة في الثقوب السوداء
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















