
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Electrodynamics in a homogeneous gravitational field
المؤلف:
Heino Falcke and Friedrich W Hehl
المصدر:
THE GALACTIC BLACK HOLE Lectures on General Relativity and Astrophysics
الجزء والصفحة:
p 164
2-2-2017
1921
Electrodynamics in a homogeneous gravitational field
1.1 Electrodynamics in the uniformly accelerated frame
In order to study the properties of the electromagnetic field in the black hole vicinity it is instructive to neglect effects connected with curvature at first. Since the curvature near the horizon is ∼M−2, where M is the black hole mass, this limit corresponds formally to the case of M → ∞. For an observer at rest near the horizon of such a black hole, the gravitational field is almost homogeneous. According to the equivalence principle, physical laws in the reference frame of the observer mentioned before are identical to the laws in flat spacetime considered in a uniformly accelerated reference frame. Let us discuss now a formulation of the standard electrodynamics in a uniformly accelerated frame.
Consider an accelerated observer in flat spacetime in Rindler coordinates,
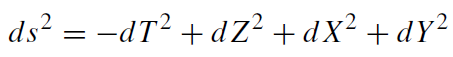 (1.1)
(1.1)
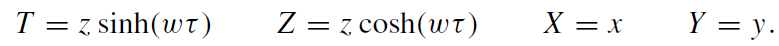 (1.2)
(1.2)
The accelerated observer is located at z = w−1, and w and τ are the four
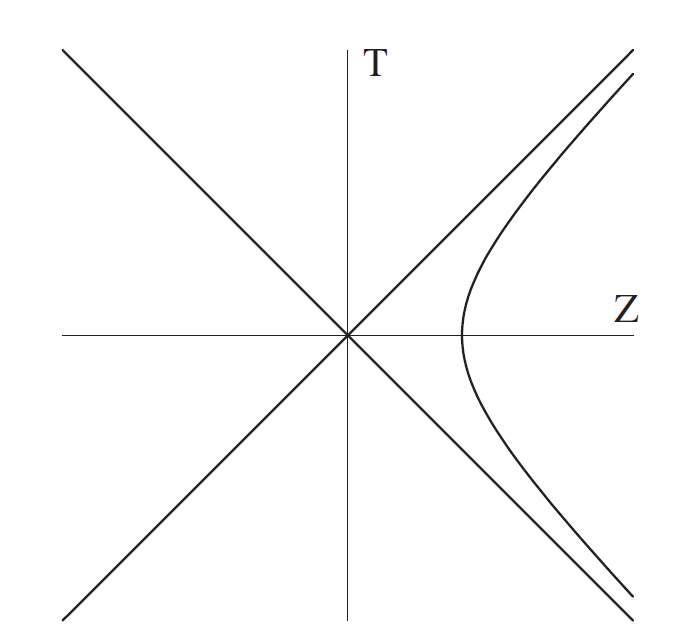
Figure 1.1. Rindler spacetime.
acceleration and proper time of the observer, respectively. The coordinates (τ, x, y, z) cover the right wedge X > |T | of the Minkowski spacetime. The null surface U = T − X = 0 plays the role of the event horizon, since the observer cannot get any information from the region U > 0 lying beyond it.
The electrodynamics in the accelerated frame is described by the standard Maxwell equations
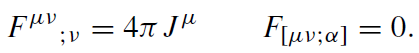 (1.3)
(1.3)
Since nothing that happens beyond the horizon affects the information available to the observer, let us simply assume that Fμν vanishes in this region. Substituting the ansatz ˜Fμν = FμνΘ(U) into the Maxwell equations one gets
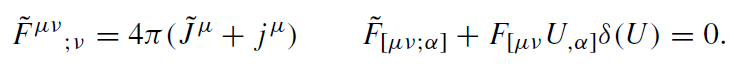 (1.4)
(1.4)
Here Ĵμ = JμΘ(U) and
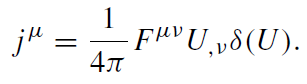 (1.5)
(1.5)
This equation shows that in order to have a vanishing field beyond the horizon there must be an additional surface current jμ. We call this current fictitious. We introduce it only in order to mimic the correct electromagnetic field outside the horizon. Certainly, any observer crossing the horizon will not see any currents until there are real charged particles crossing the horizon. Since jμU,μ = 0 this current is propagating along the horizon. One also has
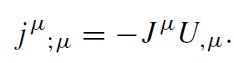 (1.6)
(1.6)
Thus, the fictitious current is conserved until real charged particles cross the horizon.
1.2 Fictitious horizon currents for an accelerated charge
Let us consider a simple example. Suppose a pointlike electric charge q is moving with a constant acceleration w in the Z-direction. Using a standard solution of this problem in the form of the Lienard-Wiechert potentials, one can obtain the non-vanishing components of the field strength:
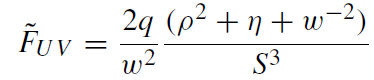 (1.7)
(1.7)
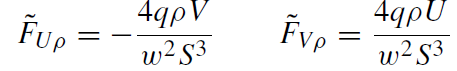 (1.8)
(1.8)
where
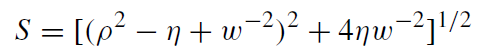 (1.9)
(1.9)
 (1.10)
(1.10)
Simple calculations show that at the surface U = 0 there is only one non-vanishing component of the fictitious current
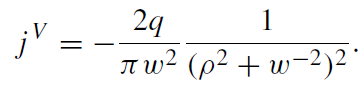 (1.11)
(1.11)
Thus, one has an axisymmetric distribution of a negative fictitious charge density
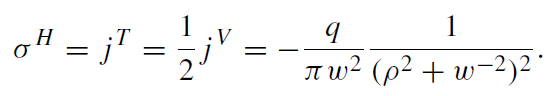 (1.12)
(1.12)
We took into account that T = V/2 at the surface U = 0. It is easy to check that the integral of σ over the total X–Y plane is −q.
1.3 Electric charge in the homogeneous gravitational field
According to the equivalence principle physical laws in the static homogeneous gravitational field are equivalent to the laws found in a uniformly accelerated frame in flat spacetime. For our concrete case, this means the following. Let us write the flat metric in Rindler coordinates
ds2 = −z2w2 dτ 2 + dz2 + dx2 + dy2. (1.13)
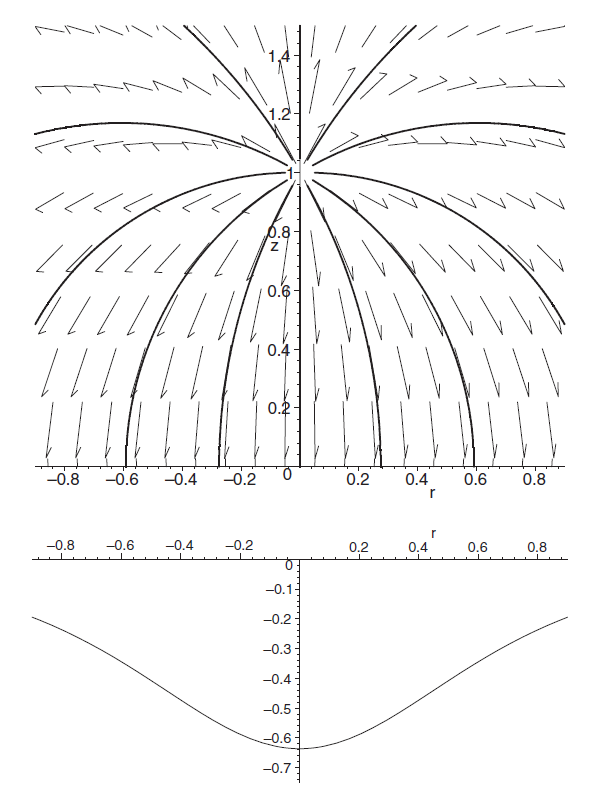
Figure 1.2. Electric field of a pointlike charge in a homogeneous gravitational field and the corresponding fictitious charge density on the horizon.
A pointlike electric charge q is at rest in this gravitational field at the point (w−1, 0, 0) and its electric potential is
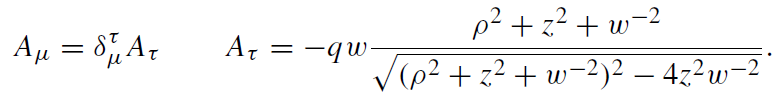 (1.14)
(1.14)
This is a solution of Maxwell’s equations in the Rindler metric:
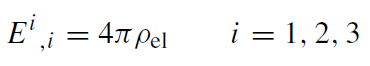 (1.15)
(1.15)
Ei = (wz)−1Aτ,i is the (three-dimensional) electric field and ρel = wz Jτ .
Integral lines of the vector field Ei are shown in figure 1.2. These lines are orthogonal to the horizon. The induced negative fictitious charge density on the horizon is equal to σ H = Ez(z = 0)/4π and it coincides with the expression given in the previous section. This relation can be considered as a boundary condition at the horizon. It resembles the boundary condition at a conducting surface. In the next section we discuss this analogy in more detail.
Let us assume now that the electric charge q slowly moves away from the horizon and then returns to its initial position. Let v = τ +ln(wz) be an advanced time. We can rewrite the conservation law for the fictitious currents on the horizon as
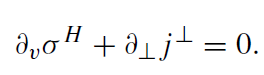 (1.16)
(1.16)
This equation can be integrated for an arbitrary function w(τ) with the following result
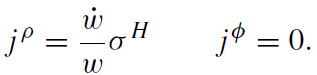 (1.17)
(1.17)
 الاكثر قراءة في الثقوب السوداء
الاكثر قراءة في الثقوب السوداء
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















