
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Mechanism of the power generation
المؤلف:
Heino Falcke and Friedrich W Hehl
المصدر:
THE GALACTIC BLACK HOLE Lectures on General Relativity and Astrophysics
الجزء والصفحة:
p 176
2-2-2017
1945
Mechanism of the power generation
1.1 Potential difference
The potential difference between the (north) pole of the black hole and its equator, as measured by an stationary observer vμ ∼ ξμ(t )+ ΩFξμ(φ), is
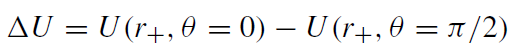 (1.1)
(1.1)
 (1.2)
(1.2)
One has
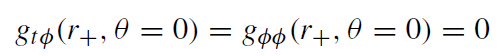 (1.3)
(1.3)
 (1.4)
(1.4)
Thus
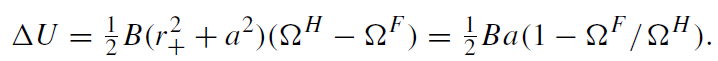 (1.5)
(1.5)
For a stationary observer co-rotating with a black hole ΔU vanishes. For ΩF ≠ ΩH there is a non-vanishing electric potential.
One can easily ‘predict’ this effect by using the analogy of a black hole horizon with a conducting surface with the effective surface resistance RH = 4π/c = 377 Ω. It is well known that a rotation of a metallic conducting sphere in an external homogeneous magnetic field generates a difference in the potentials between the pole and the equator of the sphere. Such a device is known as a unipolar inductor.
1.2 Black hole magnetosphere and efficiency of the power generating process
Astrophysical black holes are surrounded by plasma. In the most important case for astrophysics, the conductivity of the plasma is so high that the electric field in the reference frame, comoving with the plasma, vanishes, and the magnetic lines of force are ‘frozen’ into the plasma. In this case, the electric and magnetic fields in an arbitrary reference frame are perpendicular to each other (degenerate fields):
E · B = 0. (1.6)
Note that this condition is only an approximation and generally a small longitudinal electric field is present. To solve problems concerning the configuration of fields, currents, and charge distributions, it is only necessary that the inequality
|E · B| << |E2 − B2| (1.7)
is satisfied. Small deviations from the exact equation in the neighborhood of a black hole may prove to be important for a number of astrophysical processes. To simplify the problem, it is usually assumed that the system (a black hole, surrounding plasma, and the electromagnetic field) is stationary and axisymmetric.
Denote by ṽμ a vector of an observer comoving with the plasma. Then one has
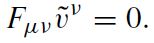 (1.8)
(1.8)
In the reference frame of this observer, the electric field vanishes. This property is also valid for any frame which is moving with respect to ṽμ with the velocity along the magnetic field. Let us choose a special solution of equation (1.8) which meets the symmetry property
 (1.9)
(1.9)
where ΩF is a function of r and θ. Let us stress that the vector ṽμ, which has evident physical meaning, must always be timelike, while the vector vμ can be spacelike. This happens near the horizon if ΩF ≈ ΩH.
In the force-free approximation, the rotational energy of the black hole is extracted
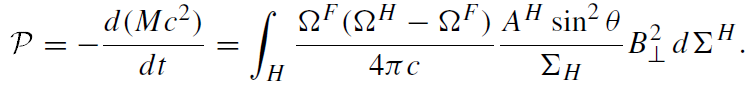 (1.10)
(1.10)
This energy is transferred along magnetic lines of force into a region located far away from the black hole where the force-free condition is violated; energy is pumped into accelerated particles, and so forth.
The power is maximal when ΩF = ΩH /2. Macdonald and Thorne demonstrated that this condition is likely to be implemented in the described model.
In order of magnitude, the power of the ‘electric engine’ outlined here is
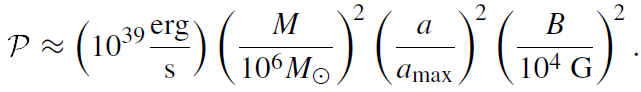 (1.11)
(1.11)
Here B is the magnetic field strength in the neighborhood of the black hole. Sometimes this electric engine is described in terms of concepts taken from electrical.
1.3 Black hole as a unipolar inductor
The lines of constant θ are equipotential curves at the horizon since the field EH is meridional. Hence, the potential difference between two equipotential lines (marked by l and 2) is
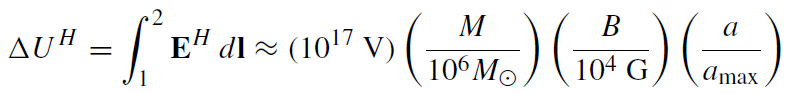 (1.12)
(1.12)
where d l is the distance element along a meridian of the black hole surface and ΔUH is the difference between the values of UH on the equipotentials 1 and 2. The approximate equality is valid if ΩF ≈ ΩH /2, maximal ΩH, and the equipotentials 2 and 1 corresponding to the equatorial and polar regions, respectively.
However, ΔUH can be written in terms of the surface current iH and resistance:
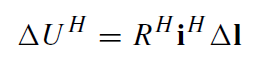 (1.13)
(1.13)
where Δl is the distance along the meridian between the equipotentials 2 and 1. Substituting the expression for iH, we obtain
 (1.14)
(1.14)
where
 (1.15)
(1.15)
is the total resistance between the equipotential lines 2 and 1. (If the equipotentials 2 and 1 correspond to the equator and to θ ≈ π/4, the integration of (1.15) yields ΔZ H ≈ 30 Ω).
These formulas permit the conclusion that in this model the rotating black hole acts as a battery with an e.m.f. of order
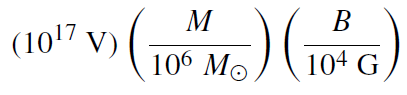 (1.16)
(1.16)
and an internal resistance of about 30 Ω.
This mechanism (and a number of its variants) has been employed in numerous papers for the explanation of the activity of the nuclei of galaxies and quasars.
 الاكثر قراءة في الثقوب السوداء
الاكثر قراءة في الثقوب السوداء
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















