1.1 Killing vectors

A Killing vector field ξ^μ is a vector field which satisfies the Killing equation

 ξ(μ;ν) = 0. (1.1)

A Killing vector is a generator of a symmetry transformation on a spacetime manifold. Killing trajectories are integral lines of the Killing vector field,

 (1.2)

If ξ^μ is regular, Killing trajectories form a foliation and one can introduce (at least locally) coordinates (t, yⁱ ) where t is a parameter along the trajectory, and the yⁱ are constant on a given trajectory. It is easy to show that the metric g_μν in these coordinates does not depend on t. This demonstrates explicitly the symmetry of the spacetime carrying a Killing vector.

1.2 Integrals of motion

For a geodesic motion the quantity ξ_μ u^μ is constant along the particle world line and hence it is an integral of motion. This follows from

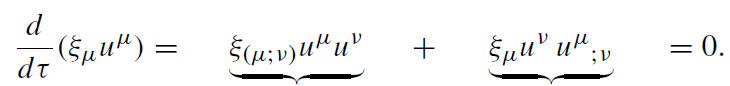 (1.3)

1.3 Symmetries of Schwarzschild spacetime

Being static and spherically symmetric, the Schwarzschild metric has four linearly independent Killing vector fields. One of them, in Schwarzschild coordinates,

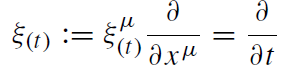 (1.4)

is connected with the time symmetry. The other three are generators of the three parameter group of rotations preserving the geometry on a unit sphere:

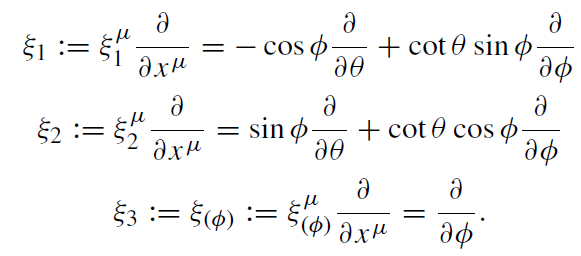 (1.5)

The latter vector generates rotation around a z-axis passing through the north θ = 0 and south θ = π poles of the black hole.

The Killing vector ξ(t ) possesses the following properties:

● ξ(t ) is orthogonal to the surface t = constant. This property follows from the invariance of the metric with respect to time reflection t → -t. (The metric is not only stationary but also static.)

● The infinite redshift surface where ξ²_(t) = g_{t t} = 0 coincides with a Killing horizon, which in its turn coincides with the event horizon, see later.

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم الإعلام يشارك في الاجتماع التحضيري لمناقشة الخطة الإعلامية لزيارة عاشوراء

بحضور متوليها الشرعي.. العتبة العباسية المقدسة تواصل إقامة المجالس الحسينية لإحياء شهر المحرم

قسم الشؤون الفكرية يطلق برنامجه التبليغي في أكثر من 20 دولة إفريقية

شعبتا الخطابة النسوية والتوجيه الديني تواصلان إقامة المجالس الحسينية في مرقد أبي الفضل العباس (عليه السلام)

المزيد

الآخبار الصحية

دراسة تكشف علاقة خطيرة بين عمر الأم وصحة مولودها

دراسة تحذر.. اضطراب نوم بسيط قد يسبب الموت المبكر ؟

الاستحمام بالماء الساخن.. راحة مؤقتة وأضرار دائمة للبشرة

ماذا يحدث للجسم عند تخطي وجبة الإفطار؟

المزيد

الآخبار التكنلوجية

كيف تساعد الصيانة الوقائية في الحفاظ على كفاءة التكييف في سيارتك ؟

في ظاهرة غريبة حيرت العلماء.. كوكبنا قد يسجل أقصر يوم في التاريخ هذا الصيف!

السد الصيني العملاق يعيق دوران الأرض ويغيّر شكلها ؟

السعودية تطلق 10 تجارب علمية إلى محطة الفضاء الدولية

المزيد

مواضيع ذات صلة

الأسرار المتبقية للثقوب السوداء ( نهاية الزمكان أم بوابة لكون آخر؟)

الثقوب الدودية

الثقوب البيضاء

الثقوب السوداء العملاقة

الثقوب السوداء

الثقوب السوداء

الطبيعة المتفردة للجاذبية

يمكن كشف التموجات الناتجة عن تصادم الثقوب السوداء في الفضاء

لماذا ندرس الثقوب السوداء؟

ماذا يحدث عند سقوط ثقب أسود في ثقب أسود؟

إطلاق النفثات

جمال التناظر