We consider only a special type of motion off the equatorial plane when particles are moving quasiradially along the trajectories on which the value of the polar angle θ remains constant, θ = θ₀. For this motion

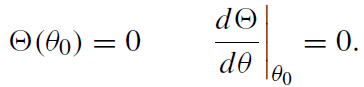 (1.1)

If we exclude trivial solutions θ₀ = 0, θ₀ = π, and θ₀ = π/2, the relations between the integrals of motion can be written in the form

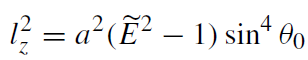 (1.2)

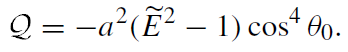 (1.3)

Hence, motion with constant θ = θ₀ is possible only when Ẽ > 1 (infinite motion).

Non-relativistic particles moving at parabolic velocity (v_∞ = 0) and with zero angular momentum (l_z = 0) represent a special limiting case. Such particles fall at constant θ and are dragged into the rotation around the black hole.

Another important limiting case is the falling of ultrarelativistic particles (photons) which move at infinity at θ = constant. In this limit, Ẽ → ∞and l_z →∞ while their ratio b = l_z/Ẽ remains finite and equal to b = a sin2 θ. The null vector n^μ tangent to a null geodesic representing the motion of the in-coming photon is

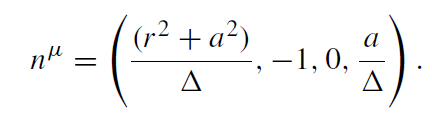 (1.4)

If one substitutes 1 instead of −1 into the right-hand side of this expression one obtains a congruence of outgoing photons. These two null congruences are known as the principal null congruences of the Kerr metric. They are geodesic and shear free. They satisfy the following relations:

 (1.5)

where C_{αβγ δ} is the Weyl tensor. Since the Kerr metric is a vacuum solution, the Weyl tensor is equal to the Riemann tensor. The principal null vectors in the Kerr geometry also obey the relation

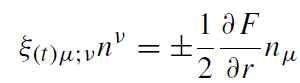 (1.6)

where F = -g_{t t} = 1 - 2Mr/Σ.

اخر الاخبار

اخبار العتبة العباسية المقدسة

عباس.. طفل فقد والده فوجد في خدمة زائري عاشوراء وطنًا آمنًا

شعبة الخطابة النسوية تواصل إقامة مجالس العزاء في شهر المحرم الحرام

لليوم الخامس.. العتبة العباسية المقدسة تقيم مجلس عزاء في صحن مرقد أبي الفضل العباس (عليه السلام)

قسم الشؤون الفكرية يقيم مجلس عزاء حسيني في العاصمة التنزانية دار السلام

المزيد

الآخبار الصحية

لمن تجاوز الستين.. عليك بشرب 4 أكواب من القهوة يوميا ؟

الحليب مع العسل.. مزيج يمنحك 7 فوائد صحية

لا تبالغ في التنظيف.. قليل من "الاتساخ" قد يحمي عائلتك

دراسة تكشف علاقة خطيرة بين عمر الأم وصحة مولودها

المزيد

الآخبار التكنلوجية

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

كيف تساعد الصيانة الوقائية في الحفاظ على كفاءة التكييف في سيارتك ؟

في ظاهرة غريبة حيرت العلماء.. كوكبنا قد يسجل أقصر يوم في التاريخ هذا الصيف!

المزيد

مواضيع ذات صلة

الأسرار المتبقية للثقوب السوداء ( نهاية الزمكان أم بوابة لكون آخر؟)

الثقوب الدودية

الثقوب البيضاء

الثقوب السوداء العملاقة

الثقوب السوداء

الثقوب السوداء

الطبيعة المتفردة للجاذبية

يمكن كشف التموجات الناتجة عن تصادم الثقوب السوداء في الفضاء

لماذا ندرس الثقوب السوداء؟

ماذا يحدث عند سقوط ثقب أسود في ثقب أسود؟

إطلاق النفثات

جمال التناظر