
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Wave fields in the Kerr metric
المؤلف:
Heino Falcke and Friedrich W Hehl
المصدر:
THE GALACTIC BLACK HOLE Lectures on General Relativity and Astrophysics
الجزء والصفحة:
p 157
2-2-2017
1571
Wave fields in the Kerr metric
1.1 Electromagnetic waves and gravitational perturbations in the Kerr geometry
The scalar massless field we have considered is a toy model. For astrophysical applications it is important to understand the behavior of electromagnetic waves and (in view of coming gravitational wave experiments) gravitational perturbations. Aspects of the problem connected with the black hole rotation also might be important. Fortunately, as demonstrated by Teukolsky, the initial set of equations, which describes electromagnetic waves or gravitational perturbations in the Kerr metric, can be reduced to a form which allows decoupling. Moreover, the resulting decoupled equations allow separation of variables. We describe here only the scheme and the main result, omitting details and long calculations.
The homogeneous equations describing electromagnetic waves or gravitational perturbations propagating in an external gravitational field are of the form
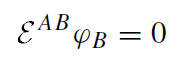 (1.1)
(1.1)
where ƐAB is a covariant differential operator, and A and B represent collective tensorial indices. For the electromagnetic field
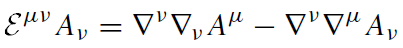 (1.2)
(1.2)
and for gravitational perturbations
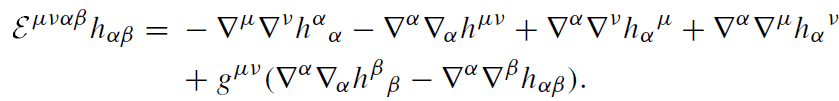 (1.3)
(1.3)
1.2 Field equation decoupling. Teukolsky equation
In the Kerr metric these equations (as well as the equations for other massless fields with spin s) can be decoupled. This means that there exist three operators (we denote them sτA, sПB, and s □) such that the following relation is valid:
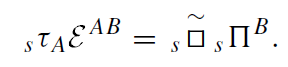 (1.4)
(1.4)
Here s = 0,±1/2,±1,±3/2,±2, and |s| is the spin of the field φA. For electromagnetic waves |s| = 1 and for gravitational perturbations |s| = 2. Relation (1.4) shows that the scalar sψ = sПBφB, constructed for any solution of the equation ƐABφB = 0, obeys the scalar decoupled equation
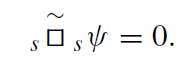 (1.5)
(1.5)
Usually the covariant operator s□ is presented in the form
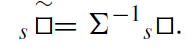 (1.6)
(1.6)
We recall that in the Kerr metric √−g = Σ sin θ. The scalar second-order differential operator s□ was introduced by Teukolsky. Its explicit form depends on the choice of coordinates and complex null tetrads. In Boyer– Lindquist coordinates and for the so called Kinnersley tetrad, the operator s□ is specified by
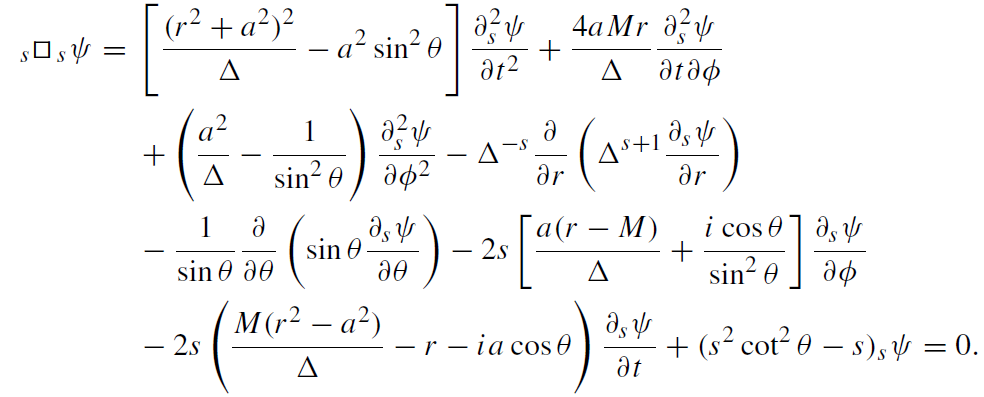 (1.7)
(1.7)
This is the so called Teukolsky equation.
1.3 Field restoration from solutions of the decoupled equations
A solution of the tensor field equation can be constructed from the solutions of the related Teukolsky equation. This was demonstrated by Cohen and Kegels for the electromagnetic field and by Chrzanowski for gravitational perturbations. Wald gave a simple proof of a general result which shows how to construct a field once one has succeeded in deriving a decoupled equation.
In order to describe the idea of this proof, let us introduce a scalar product of two (generally complex) tensor fields ψA and φA
 (1.8)
(1.8)
The action W[φ] for a real tensor field ϕ obeying the field equation can then be written in the compact form
 (1.9)
(1.9)
Further denote by Q an operator which is conjugated to an operator Q with respect to the scalar product
an operator which is conjugated to an operator Q with respect to the scalar product
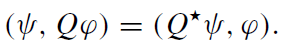 (1.10)
(1.10)
The operator Ɛ is then self-conjugated Ɛ = Ɛ. By using this property we can rewrite the equation obtained by conjugation in the form
= Ɛ. By using this property we can rewrite the equation obtained by conjugation in the form
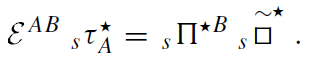 (1.11)
(1.11)
It can be shown that
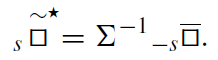 (1.12)
(1.12)
This relation shows that for any solution sΞ of the scalar equation
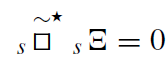 (1.13)
(1.13)
the tensor function
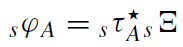 (1.14)
(1.14)
is a solution to the field equation. Moreover, it can be shown that all such solutions (up to possible gauge transformation) can be represented in this form. Thus, solutions to the scalar decoupled equation provide complete information about the perturbing field.
1.4 Separation of variables, spin-weighted spheroidal harmonics
The coefficients of the Teukolsky equation do not depend on t and φ. Furthermore, the existence of the Killing tensor in Kerr spacetime yields an additional symmetry of the Teukolsky equation which makes it possible to solve it by separation of variables and to write a solution in terms of the modes
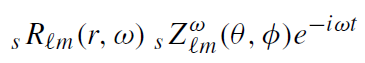 (1.15)
(1.15)
where sZωℓm(θ, φ) are the spin-weighted spheroidal harmonics
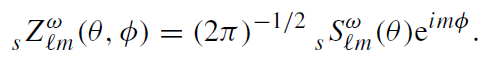 (1.16)
(1.16)
The angular problem reduces to one of solving
 (1.17)
(1.17)
where the functions sSℓm(θ ) are regular on the interval [0, π].
The required functions sSℓm (θ ) thus essentially follow from a Sturm– Liouville eigenvalue problem for the separation constant E. Boundary conditions of regularity should be imposed at both θ = 0 and π. According to Sturm– Liouville theory, the eigenfunctions form a complete, orthogonal set on the interval 0 ≤ θ ≤ π for each combination of s, aω and m. This infinite set of eigenfunctions is enumerated by ℓ. For a = 0 and s = 0 functions sSℓm (θ ) coincide with the associated Legendre polynomials Pmℓ (cos θ).
1.5 The radial equation
The radial functions sRℓm obey a second-order differential
 (1.18)
(1.18)
where
 (1.19)
(1.19)
An important property of the radial Teukolsky equation is that the two solutions sRℓm and −sRℓm.
Introducing a new dependent variable
 (1.20)
(1.20)
the radial equation can be written in the form
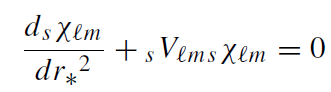 (1.21)
(1.21)
which is similar to the form of the radial equation for a scalar massless field in the Schwarzschild geometry. Nevertheless there are important differences. The effective potential sVℓm is
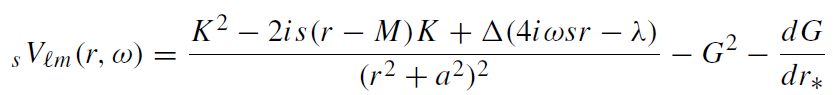 (1.22)
(1.22)
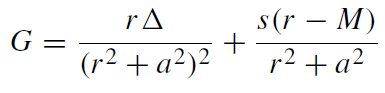 (1.23)
(1.23)
and r∗ is the ‘tortoise’ coordinate defined by
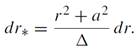 (1.24)
(1.24)
This potential is complex and it depends on the frequency ω. In the asymptotic regions (r∗ →±∞) the potential sVℓm takes the form
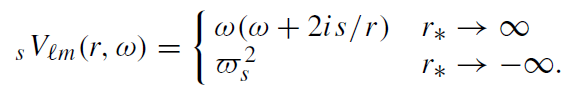 (1.25)
(1.25)
Here
 (1.26)
(1.26)
and κ = (r+ − M)/(r2++ a2) is the surface gravity of the Kerr black hole. Two linearly independent solutions have the asymptotic behavior ∼ r∓s exp(±iωr∗) at r →∞ and ∼ Δ±s/2 exp(±iϖr∗) at r →r+.
1.6 Modes
In the same manner as it was done for a massless scalar field in the Schwarzschild geometry, solutions to the equations describing a free massless field in the exterior of a Kerr black hole can be specified by prescribing their asymptotics at null infinity and the horizon. It is possible to introduce four sets of solutions called IN, UP, OUT, and DOWN modes, correspondingly in the same manner as it was done for the Schwarzschild spacetime.
Each of the modes is a solution characterized by the set {ℓmωP} of quantum numbers, where the spirality P = ±1. These modes are singled out by the following requirements: IN modes vanish at H− and have non-vanishing asymptotics at 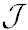 −. UP modes vanish at
−. UP modes vanish at 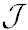 − and are non-vanishing on the past horizon H−. OUT modes vanish at H+ but not at
− and are non-vanishing on the past horizon H−. OUT modes vanish at H+ but not at 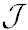 +, and finally the DOWN modes vanish at
+, and finally the DOWN modes vanish at 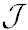 + and are non-vanishing on the past horizon H+. Any two of these four solutions can be used as a complete set in the space of solutions.
+ and are non-vanishing on the past horizon H+. Any two of these four solutions can be used as a complete set in the space of solutions.
 الاكثر قراءة في الثقوب السوداء
الاكثر قراءة في الثقوب السوداء
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















