
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
A relaxed stellar system around a MBH
المؤلف:
Heino Falcke and Friedrich W Hehl
المصدر:
THE GALACTIC BLACK HOLE Lectures on General Relativity and Astrophysics
الجزء والصفحة:
p 251
6-2-2017
3075
A relaxed stellar system around a MBH
The relaxed, quasi steady-state density distribution of a single-mass stellar population around a MBH is (Bahcall and Wolf 1976, see also Binney and Tremaine 1987 for a simple derivation)
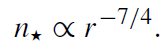 (1.1)
(1.1)
When the stellar population consists of a spectrum of masses, M1 < M* < M2, the stellar distribution function (DF) very near the MBH has the form (Bahcall and Wolf 1977)
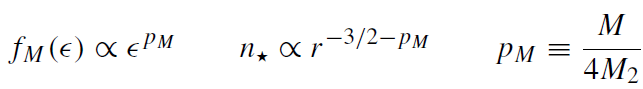 (1.2)
(1.2)
where -ϵ is the total specific energy of the star and fM ≡ 0 for ϵ < 0. The velocity dispersion of this DF (see equation (1.5)) is almost independent of the stellar mass,
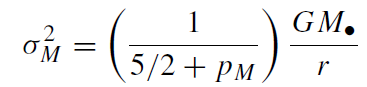 (1.3)
(1.3)
which implies that σ2M changes by less than 10% over the entire mass range, in marked contrast to the σ2M ∝ M−1* dependence of equipartition. This result
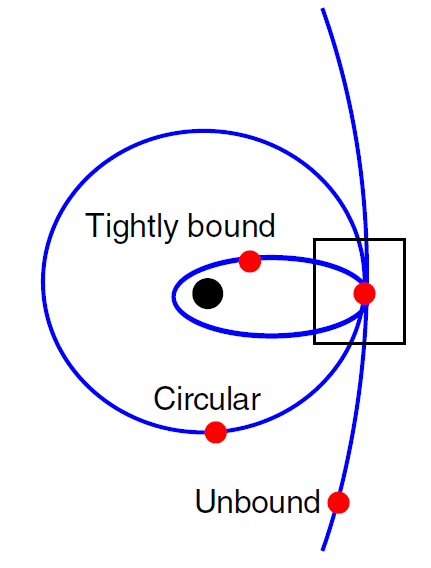
Figure 1.1. A schematic representation of the different types of stellar orbit that can be observed in a small region near the MBH.
justifies the approximation that the velocity dispersion in a relaxed stellar system around a MBH is mass independent.
The Bahcall-Wolf solution applies to point particles. This assumption no longer holds very near the MBH, where the collision rate is high because of the very high stellar density. Stars on tight orbits around the MBH cannot survive for long, and so eventually most of the population there will consist of stars that are on very wide, marginally bound (parabolic) orbits, which spend only a small fraction of their time in the collisionally dominated region. These marginally bound stars have a flatter spatial distribution, of the form (e.g. Binney and Tremaine 1987)
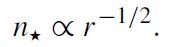 (1.4)
(1.4)
The stars in any volume element near the MBH have a distribution of orbits (figure 1.1): some are more bound than circular (i.e. their velocity is smaller than the circular velocity vc), some are less bound than circular, some are unbound to the MBH (but bound by the total mass of the MBH and stars). The distribution of orbits is directly tied to the spatial distribution through the Jeans equation,
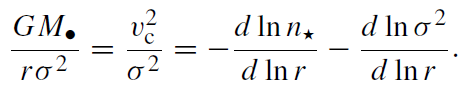 (1.5)
(1.5)
The Jeans equation is essentially a re-statement of the continuity equation of the stellar orbits in phase space in terms of averaged quantities, the mean stellar density and velocity dispersion. Here it is given for the simplest case of a steady state, isotropic, non-rotating system. The steady state assumption is justified
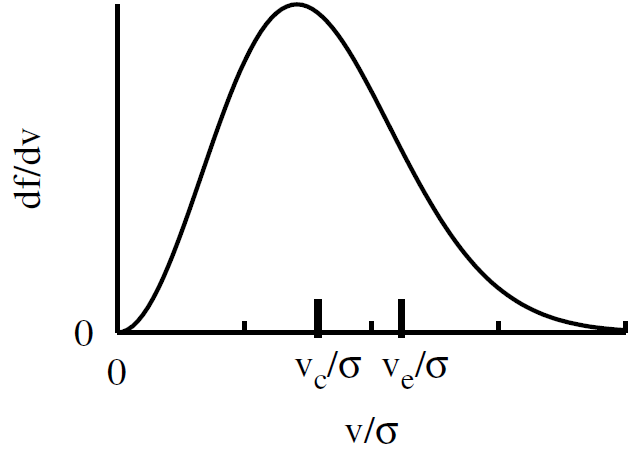
Figure 1.2. The fraction of orbits in the Maxwell-Boltzmann distribution as a function of the normalized velocity v/σ. The circular velocity vc and the escape velocity ve = √2vc are marked for a density distribution with α = 1.5. The region v > ve lies under the exponential tail of the DF, and so the fraction of stars with unbound orbits is a strongly decreasing function of α.
because the dynamical timescale is much shorter than the relaxation timescale. The assumptions of approximate isotropy and non-rotation are observationally justified.
Very near the MBH the velocity dispersion is Keplerian, σ2 ∝ r−1, and so for any power-law cusp n* ∝ r−α, the Jeans equation implies that
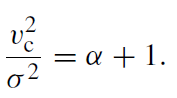 (1.6)
(1.6)
The steeper the cusp (larger α) is the larger the ratio between vc and σ, and so the fraction of loosely bound stars or unbound stars is smaller (figure 1.2). Because unbound stars have wide orbits and spend most of their time far away from the MBH, the stellar population in a shallow cusp is well mixed and representative of the average population over a large volume. In contrast, the stellar population in a steep cusp is localized and can therefore develop and maintain properties that differ from those of the general population.
 الاكثر قراءة في الثقوب السوداء
الاكثر قراءة في الثقوب السوداء
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















