
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Physical scales
المؤلف:
Heino Falcke and Friedrich W Hehl
المصدر:
THE GALACTIC BLACK HOLE Lectures on General Relativity and Astrophysics
الجزء والصفحة:
p 249
6-2-2017
1473
Physical scales
There are several important timescales and length scales that govern the dynamics of the stellar system and MBH. They are listed here with estimates of their value in the Galactic Center. A solar-type star and M● = 3 × 106 Mּ (Genzel et al 2000) are assumed throughout. Physical lengths are also expressed as angular sizes assuming that the distance to the Galactic Center is R0 = 8 kpc (Reid 1993).
1.1 Timescales
The dynamical time, or orbital time, td, is the time it takes a star to cross the system
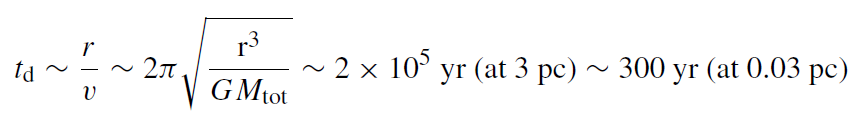 (1.1)
(1.1)
where r is the typical size of the system and Mtot is the total mass enclosed in radius r .
The two body relaxation time, tr , is related to the 1D velocity dispersion σ, the mean stellar mass 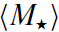 and the stellar number density n* by
and the stellar number density n* by
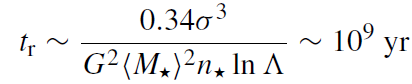 (1.2)
(1.2)
where log Λ is the Coulomb logarithm, the logarithm of the ratio between the largest and smallest impact parameters possible in the system for elastic collisions. Because the relaxation timescale in the Galactic Center is shorter than the age of the Galaxy (∼10 Gyr), the old stars are expected to be well relaxed by now.
The mass segregation timescale is of the same order as the relaxation timescale,
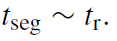 (1.3)
(1.3)
The rate (per star) of grazing collisions between two stars of mass and radius Ma* , Ra* and Mb* , Rb* , each, is
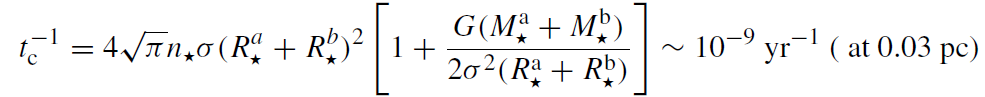 (1.4)
(1.4)
where it is assumed that the stars follow a mass-independent Maxwell-Boltzmann velocity distribution with velocity dispersion σ (this is a good approximation near the MBH). There are two contributions to the total rate, one due to the geometric cross section (first term in the square brackets) and one due to ‘gravitational focusing’ (second term in the square brackets). Gravitational focusing expresses the fact that the two stars do not move on straight lines, but are attracted to each other. This effect is important when the typical stellar velocities are much smaller than the escape velocity, ve, from the stars, σ2 < GM*/2R* = v2e /4.
1.2 Length scales
The size of the event horizon of a non-rotating black hole, the Schwarzschild radius, is
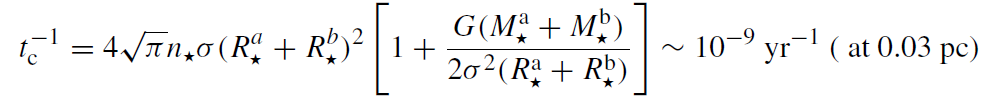 (1.5)
(1.5)
The tidal radius, rt, is the minimal distance from the MBH where the stellar self-gravity can still resist the tidal forces of the MBH. If the star's orbit takes it inside the tidal radius, it will be disrupted, and roughly half of its mass will fall into the MBH, while the other half will be ejected (e.g. Ayal et al 2000). The exact value of the tidal radius depends on the stellar structure and the nature of the orbit, and up to a factor of order unity is given by
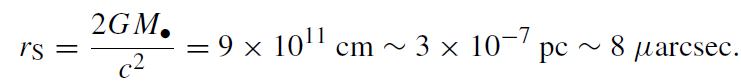 (1.6)
(1.6)
Tidal disruption is relevant as long as the tidal radius lies outside the event horizon. Since rt ∝ M●1/3, while rS ∝ M●, there exists a maximal MBH mass for tidal disruption, which for a solar-type star is ∼108 Mּ.
The radius of influence, rh, is the region where the MBH potential dominates the dynamics. If the MBH is embedded in an isothermal stellar system (i.e. σ is constant), then the radius of influence can be defined as
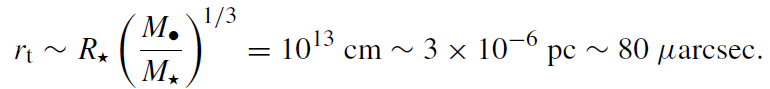 (1.7)
(1.7)
In practice, the distribution is not isothermal and σ is not constant, and so rh is evaluated loosely by choosing a representative value of σ far enough from the MBH. The stellar mass enclosed within rh is of the same order as the mass of the MBH.
 الاكثر قراءة في الثقوب السوداء
الاكثر قراءة في الثقوب السوداء
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















