Once the radial profiles (optical depth, density, velocity, and temperature) are determined, it is possible to calculate the emission spectrum for a given magnetic field profile. The predicted observable luminosity L_ν0 at infinity (Shapiro 1973, Melia 1992) with relativistic corrections is

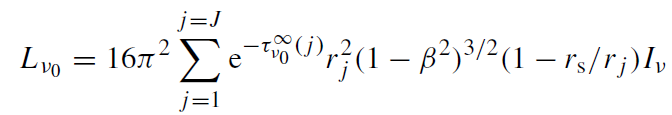 (1.1)

where

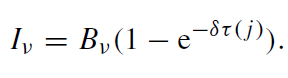 (1.2)

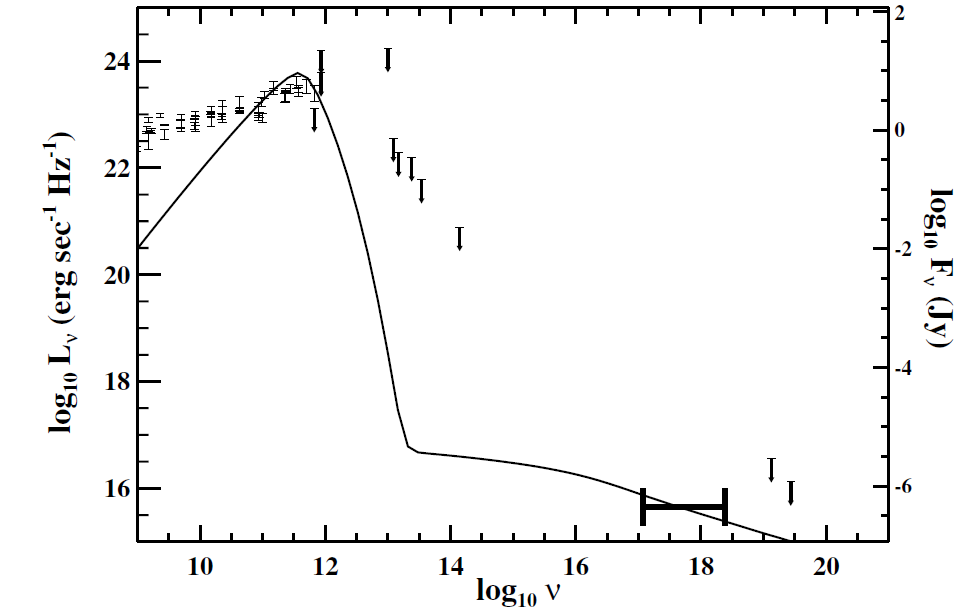
Figure 1.1. The full curve is an example spectrum profile from (1.1) with parameters but with δ_B = 0.001. Also shown are the observed values and upper limits with the recent Chandra results (Baganoff et al 2001a, b) highlighted in bold. At a distance of 8.5 kpc, for Galactic Center sources F_ν 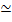 10²³L.

The sum over j is truncated at J, for which r_J ≡ R_A. It is assumed thatτ^∞_ν0 (J ) = 0. This ignores the possible absorption by Sgr A West of the low frequency (ν₀ < 10⁹ Hz) radiation (Beckert et al 1996). Sgr A West is an H II region surrounding Sgr A^*.

An example of a spectrum arising from these equations is shown in figure 1.1. Although only a representative solution, the primary features of all spherical accretion models are apparent. First, there is little emission in the infrared, unlike disk accretion scenarios where the gas circularizes and thermalizes before accreting. Second, there is significant X-ray emission due to thermal bremsstrahlung. However, in the case of Sgr A^*, the observed quiescent X-ray spectrum is too soft to be due to thermal bremsstrahlung alone; the sub-mm emission, coming from very close to the black hole, is likely to be upscattered via inverse Compton and produce additional X-ray emission. Third, the spectral index in the radio is ∼1, rather steeper than the observed value of ∼0.3 (Falcke et al 1998). This last characteristic deserves some attention.

If the gas temperature and density profiles are at all similar to the Bondi-Hoyle results given earlier, and, if the radio emission is due to magnetic bremsstrahlung from a thermal distribution of particles, it is impossible to match both the observed 1 GHz radio flux and the soft X-ray upper limits (Liu and Melia 2001). Since the emission must be blackbody limited, one can put a lower limit on the temperature at a given radius. Similarly, the gas temperature must be less than the virial temperature, putting an upper limit on the temperature. For frequencies less than hν/k_BT , the thermal bremsstrahlung emissivity, j ^b_ν , scales as n²T ⁻¹/2 ∝ r^−5/2. Thus, the volume-integrated emissivity will increase with the size of the emission region as r ^1/2 so that the minimum luminosity corresponds to the minimum size and maximum temperature consistent with the blackbody and virial limits. Limits which result in the proper observed 1 GHz flux yield a minimum radius and maximum temperature of approximately 2000 rs and 10⁹ K, respectively. Since the soft X-ray emission is not likely to be self-absorbed while the GHz emission may be, the ratio of the volume integrated emissivities must be less than the ratio of the observed fluxes. For an equipartition type magnetic field profile, the result is that the soft X-ray luminosity cannot be less than ∼10⁻⁵ times the 1 GHz luminosity. Thus, since the observed ratio is ∼10⁻⁷ (Falcke et al 1998, Baganoff et al 2001a, b), the X-ray emission cannot be due to thermal magnetic bremsstrahlung. Profiles which deviate substantially from the Bondi–Hoyle results can avoid this problem. If one assumes an inflow velocity that is larger than free-fall, for example, one can reproduce the radio and X-ray emission, even when including self-Compton (Coker and Markoff 2001). However, the most likely cause of deviation from Bondi–Hoyle is a non-spherical accretion flow so that one has effectively a radially dependent mass accretion rate. A non-thermal particle distribution due to shocks in the flow could also alter the spectrum enough to invalidate these arguments.

اخر الاخبار

اخبار العتبة العباسية المقدسة

عباس.. طفل فقد والده فوجد في خدمة زائري عاشوراء وطنًا آمنًا

شعبة الخطابة النسوية تواصل إقامة مجالس العزاء في شهر المحرم الحرام

لليوم الخامس.. العتبة العباسية المقدسة تقيم مجلس عزاء في صحن مرقد أبي الفضل العباس (عليه السلام)

قسم الشؤون الفكرية يقيم مجلس عزاء حسيني في العاصمة التنزانية دار السلام

المزيد

الآخبار الصحية

لمن تجاوز الستين.. عليك بشرب 4 أكواب من القهوة يوميا ؟

الحليب مع العسل.. مزيج يمنحك 7 فوائد صحية

لا تبالغ في التنظيف.. قليل من "الاتساخ" قد يحمي عائلتك

دراسة تكشف علاقة خطيرة بين عمر الأم وصحة مولودها

المزيد

الآخبار التكنلوجية

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

كيف تساعد الصيانة الوقائية في الحفاظ على كفاءة التكييف في سيارتك ؟

في ظاهرة غريبة حيرت العلماء.. كوكبنا قد يسجل أقصر يوم في التاريخ هذا الصيف!

المزيد

مواضيع ذات صلة

الأسرار المتبقية للثقوب السوداء ( نهاية الزمكان أم بوابة لكون آخر؟)

الثقوب الدودية

الثقوب البيضاء

الثقوب السوداء العملاقة

الثقوب السوداء

الثقوب السوداء

الطبيعة المتفردة للجاذبية

يمكن كشف التموجات الناتجة عن تصادم الثقوب السوداء في الفضاء

لماذا ندرس الثقوب السوداء؟

ماذا يحدث عند سقوط ثقب أسود في ثقب أسود؟

إطلاق النفثات

جمال التناظر