
Radiation from spherical accretion
 المؤلف:
Heino Falcke and Friedrich W Hehl
المؤلف:
Heino Falcke and Friedrich W Hehl
 المصدر:
THE GALACTIC BLACK HOLE Lectures on General Relativity and Astrophysics
المصدر:
THE GALACTIC BLACK HOLE Lectures on General Relativity and Astrophysics
 الجزء والصفحة:
p 288
الجزء والصفحة:
p 288
 8-2-2017
8-2-2017
 1923
1923
Radiation from spherical accretion
Compared to active galactic nuclei (AGNs) and even X-ray binaries (XRBs), Sgr A* is emitting very little energy for its mass; i.e. its luminosity is much less than the Eddington luminosity, the critical luminosity above which radiation pressure exceeds gravity. For Sgr A*, the former is ∼105 Lּ (Zylka et al 1995) while the latter is ∼1011 Lּ (Shapiro and Teukolsky 1983). The appeal of spherical accretion in explaining the spectrum of Sgr A* is that it is inherently inefficient, unlike most other accretion scenarios onto compact objects. For example, consider the case that the temperature and density scale as r−1 and r−3/2, respectively, and emission is only due to thermal bremsstrahlung so Λ ∝ n2T 1/2 (Rybicki and Lightman 1979). If radiative emission is thought of as a minor perturbation of the flow, one can estimate the accretion luminosity as
 (1.1)
(1.1)
or, in erg s−1,
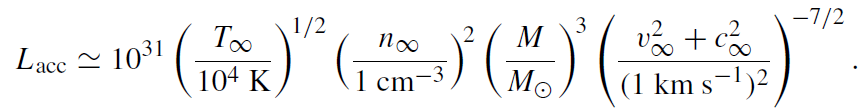 (1.2)
(1.2)
For cool, dense gas, line cooling increases the accretion luminosity, while magnetic bremsstrahlung increases the luminosity of an accreting hot magnetized plasma. Assuming just thermal bremsstrahlung, the accretion efficiency is
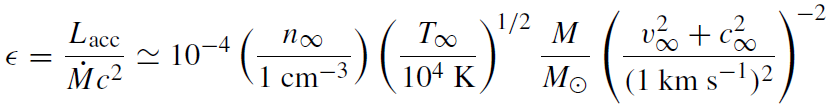 (1.3)
(1.3)
where the accretion rate is evaluated at the accretion radius. Thus, for most likely sets of values, ϵ << 0.1, the rough value for accretion disks. For the extreme case (δ = 0.03) shown, there is substantial additional luminosity due to magnetic bremsstrahlung emission, but the accretion efficiency is still only ∼4%. Thus, spherical accretion can naturally explain the sub-Eddington luminosity of Sgr A*.
If the mass accretion rate at small radii is near the Bondi-Hoyle estimate and the magnetic field is sufficiently strong, the resulting temperatures and densities at small radii are high enough that the optical depth becomes larger than unity. We can crudely estimate the optical depth, τ , for spherical accretion following Rybicki and Lightman (1979). Since we are particularly interested in τ near the event horizon, we include special and general relativisitic corrections (Shapiro 1973). Thus, δτ ( j ) 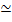 δrαabs, with
δrαabs, with
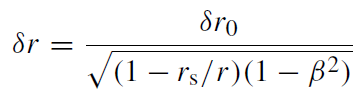 (1.4)
(1.4)
where δr0 = r j+1 − r j , the observed zone size at infinity, αabs is the absorption coefficient, and β is the bulk velocity of the flow in units of c as measured by a stationary observer:
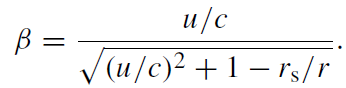 (1.5)
(1.5)
Note that this is not completely correct since we are not including, for example, the capturing of photons by the black hole, which introduces an angular dependence. For αabs, we use Kirchoff's law,
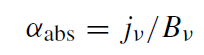 (1.6)
(1.6)
where jν is the total emissivity (in erg cm−3 s−1 Hz−1 steradian−1) and Bν is the blackbody Planck function. For the models discussed here, we use a total emissivity that includes magnetic bremsstrahlung emission (Coker and Melia 1999) and electron–ion and electron–electron thermal bremsstrahlung (Melia and Coker 1999).
In (1.6), ν corresponds to the emitted frequency, not the observed frequency. To find the total optical depth from zone j out to infinity at some observed frequency ν0, related to the emitted frequency ν by
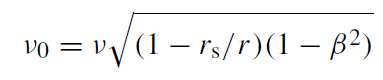 (1.7)
(1.7)
we use
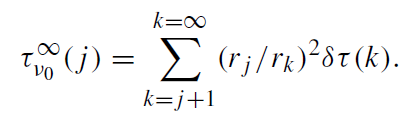 (1.8)
(1.8)
The minimum frequency νm that a photon needs to have in order to escape from radius r j is found by determining the frequency at which τ∞ν0 ( j ) is unity with the caveat that νm not be less than the plasma frequency
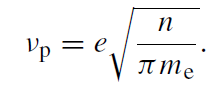 (1.9)
(1.9)
This caveat is required since photons with a frequency less than νp are unable to propagate and are thus trapped by the infalling gas. As previously mentioned, it is found that νm < 1012 Hz. Also, at νc, the characteristic frequency at which a given radius is primarily emitting, τ(r, νc) > 1 only for small radii.
 الاكثر قراءة في الثقوب السوداء
الاكثر قراءة في الثقوب السوداء
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


