
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Sub-Eddington two-temperature accretion (ADAFs)
المؤلف:
Heino Falcke and Friedrich W Hehl
المصدر:
THE GALACTIC BLACK HOLE Lectures on General Relativity and Astrophysics
الجزء والصفحة:
p 299
8-2-2017
2331
Sub-Eddington two-temperature accretion (ADAFs)
As in the previous section, we consider an axisymmetric steady-state disk accretion flow. However, the azimuthal velocity is no longer assumed to be given by the Keplerian velocity so that
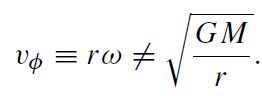 (1.1)
(1.1)
Thus, the non-relativistic equation for the radial velocity now has an extra centrifugal force term:
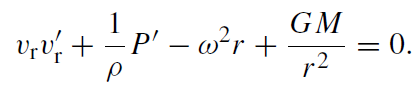 (1.2)
(1.2)
For simplicity, we will deal only with the non-relativistic equations in this section. Again, vr is defined positive for inflow. In this model, we ignore the dynamical effects of the magnetic field. The shear viscosity, ν, but is now written as
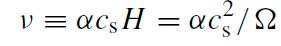 (1.3)
(1.3)
where α is the r -independent α-viscosity parameter (Shakura and Sunyaev 1973) and now cs is the isothermal sound speed (c2s≡ P / ρ = 2kBT/mp). This viscosity causes a change in ω with r which follows from the vertically integrated form of the azimuthal component of the Euler equation:
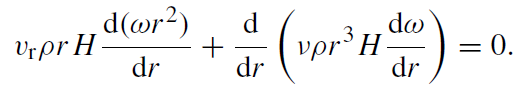 (1.4)
(1.4)
Both equations assume that the flow is viscous and therefore reduce to unphysical results (ω ∝ r−2) in the limit of ν→ 0. Using the first law of thermodynamics, written as
 (1.5)
(1.5)
where s is the specific entropy and assuming a constant γ and μ = 0.5, as
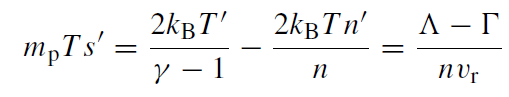 (1.6)
(1.6)
where again a prime (' ) denotes d/dr . Here, we ignore magnetic heating and instead assume that the heating is purely due to an anomalous shear viscosity so that
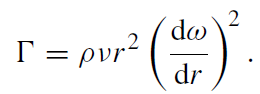 (1.7)
(1.7)
It is the ratio η ≡ Γ/Λ which determines the type of accretion flow: η 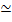 1 corresponds to the standard thin-disk solution, η
1 corresponds to the standard thin-disk solution, η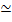 1 corresponds to the flow discussed here, and η
1 corresponds to the flow discussed here, and η 1 corresponds to Bondi-type solutions. All three types may be present near Sgr A*. In this section, we are interested in solutions in which the viscous heating rate _ is much greater than the radiative cooling rate Λ; for the Keplerian model, Γ/Λ << 1 except very close to the outer edge of the flow. The η >> 1 solutions, it turns out, require sub-Eddington mass accretion rates and a two-temperature plasma with hot ions and cool electrons. These models are known as Advection Dominated Accretion Flows (ADAFs; see Narayan et al 1998) because the ions of the gas are heated by viscous dissipation and accretion occurs before the cooler electrons can radiate. Bondi–Hoyle-type solutions also advect most of their energy without radiating (thus the low radiative efficiency described earlier) so the term ADAF is slightly misleading.
1 corresponds to Bondi-type solutions. All three types may be present near Sgr A*. In this section, we are interested in solutions in which the viscous heating rate _ is much greater than the radiative cooling rate Λ; for the Keplerian model, Γ/Λ << 1 except very close to the outer edge of the flow. The η >> 1 solutions, it turns out, require sub-Eddington mass accretion rates and a two-temperature plasma with hot ions and cool electrons. These models are known as Advection Dominated Accretion Flows (ADAFs; see Narayan et al 1998) because the ions of the gas are heated by viscous dissipation and accretion occurs before the cooler electrons can radiate. Bondi–Hoyle-type solutions also advect most of their energy without radiating (thus the low radiative efficiency described earlier) so the term ADAF is slightly misleading.
If we further assume (Ichimaru 1977, Narayan and Yi 1994, Narayan et al 1998) that Λ → 0 and α is constant with r , we find a self-similar solution exists. That is, n, T , v, and ω can be given by simple power laws: ρ ∝ r−3/2, v ∝ r−1/2, T ∝ r−1, and ω ∝ r−3/2. In particular, if A ≡ ω/_ and the Keplerian velocity is
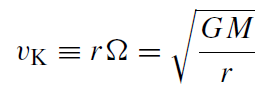 (1.8)
(1.8)
then (1.2), (1.4), and (1.6) become
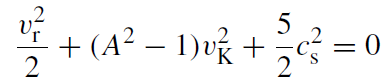 (1.9)
(1.9)
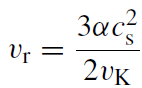 (1.10)
(1.10)
and
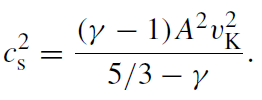 (1.11)
(1.11)
Solving these three and taking the limit α << 1 gives:
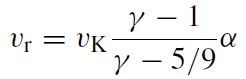 (1.12)
(1.12)
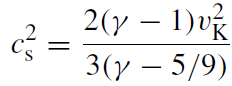 (1.13)
(1.13)
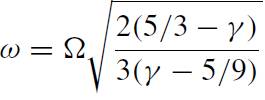 (1.14)
(1.14)
and
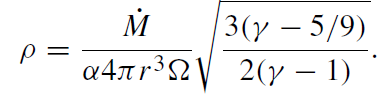 (1.15)
(1.15)
These results are similar to the profiles derived for spherical Bondi-type accretion.
In most ADAF models, it is generally assumed that a perfectly tangled magnetic field exists with a magnetic pressure that is comparable to the thermal pressure. A purely tangled field results in an added specific internal energy density term of B2/8πρ and a radial pressure term of B2/24π; this pressure is assumed to be a constant fraction (1 − βB) of the total (thermal plus magnetic) pressure. Then we have
 (1.16)
(1.16)
where Pth is the thermal component of the pressure and Ti and Te are the ion and electron temperatures (assumed equal at this point). For simplicity we assume a hydrogen mass fraction of one so that the mean molecular weights of both the ions or protons, μi, and electrons, μe are unity. The magnetic field changes the effective value of γ so that if it is assumed that the hydrodynamical adiabatic index, γad = 5/3, then
 (1.17)
(1.17)
This treatment of the field is not fully accurate since even a tangled field will also result in some resistance to the shear viscosity. In addition, the Balbus–Hawley magneto-rotational instability (Balbus and Hawley 1991) will probably eventually result in a magnetic field with a dominant azimuthal component. In the following, βB = 0.5.
A problem with self-consistency arises at this point: do the profiles given by (1.12)-(1.15) actually result in Γ >> Λ? Substituting the self-similar results gives
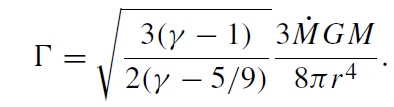 (1.18)
(1.18)
Similarly, assuming cooling is due to thermal bremsstrahlung (Rybicki and Lightman 1979) gives (in cgs units):
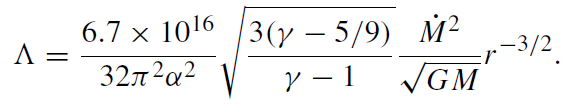 (1.19)
(1.19)
Therefore we get:
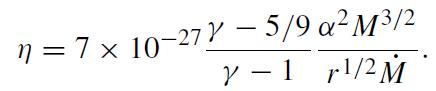 (1.20)
(1.20)
We parametrize the mass accretion rate with f ≡ ˙M / ˙ME, so that ˙M = f × 1024M6 g s−1, where ˙ME is the accretion rate that, with 10% efficiency, produces the Eddington-limited luminosity, and M6 is the mass of the black hole in units of 106Mּ. Then in order to have an ADAF solution, we must have
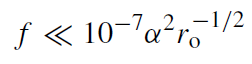 (1.21)
(1.21)
where here ro is the outer boundary of the flow in units of rs. If one includes magnetic bremsstrahlung and Compton cooling, f must be even smaller than the limit given in (1.21). Therefore, it is unlikely that large-scale single temperature ADAFs exist except in rare circumstances where the accretion rate is particularly low.
The usual way around this difficulty is to assume that the cooling is not given by (1.19) because the temperature of the radiating electrons, Te, is not the same as that of the bulk of the gas. It is argued that viscous heating applies primarily to the massive ions and the Coulomb coupling between the hot ions and cool electrons is sufficiently weak to result in a so-called ‘two-temperature plasma’. Ideally, such a problem should be solved using a full two-fluid approach, but for simplicity we shall just assume that Λ → 0 for the ions and solve explicitly for the ion and electron temperatures. Thus, instead of (10.93), Ti is given by (Esin et al 1997)
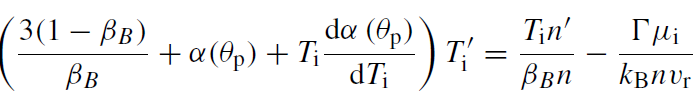 (1.22)
(1.22)
and
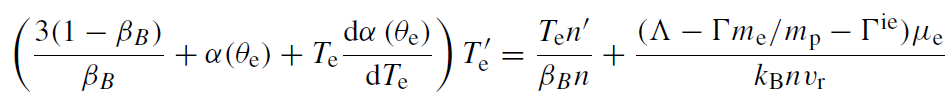 (1.23)
(1.23)
where
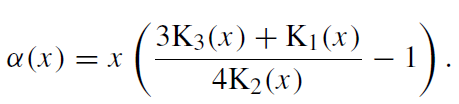 (1.24)
(1.24)
After some manipulation, it can be shown that
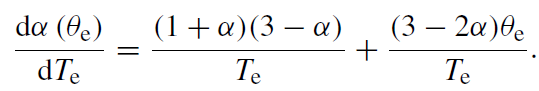 (1.25)
(1.25)
The heating of the electrons due to Coulomb coupling with the ions, Γie, is given by (Stepney and Guilbert 1983)
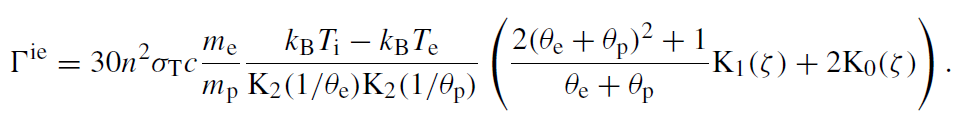 (1.26)
(1.26)
The Ki are the modified Bessel functions, σT is the Thomson cross-section, θe ≡ kBTe/mec2, θp ≡ kBTi/mpc2, and ζ ≡ (θe + θp)/θeθp. It is assumed in (1.26) that the Coulomb logarithm is  20. Since it is assumed that Ti > Te everywhere, there is no direct feedback from the electrons to the ions; since ρc2s≡ Ptot, there is indirect feedback. The profiles for the gas radial velocity, rotational frequency, and density are still given by (1.12), (1.14), and (1.15), respectively but with T = Ti. Note that in earlier work (Narayan and Yi 1995a)
20. Since it is assumed that Ti > Te everywhere, there is no direct feedback from the electrons to the ions; since ρc2s≡ Ptot, there is indirect feedback. The profiles for the gas radial velocity, rotational frequency, and density are still given by (1.12), (1.14), and (1.15), respectively but with T = Ti. Note that in earlier work (Narayan and Yi 1995a)
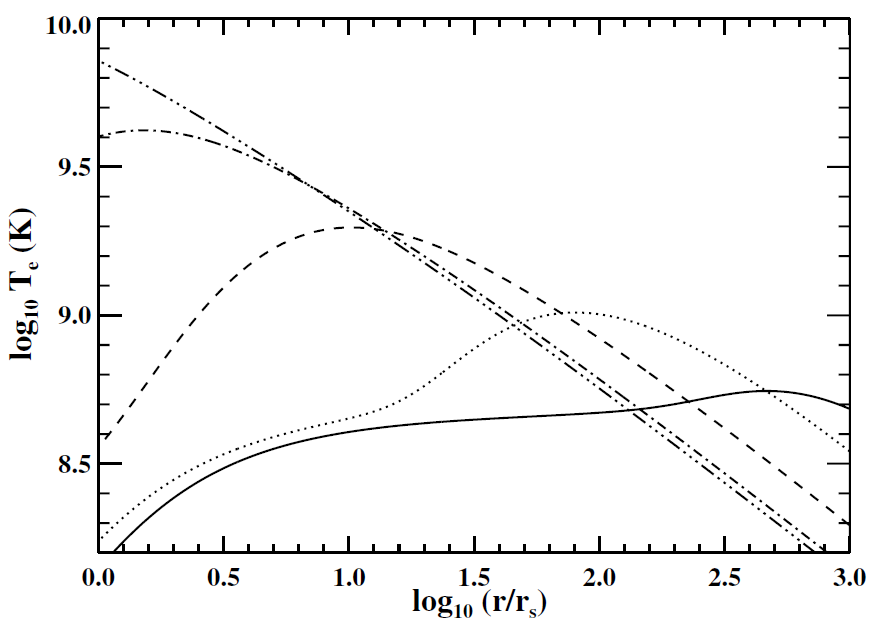
Figure 1.1. Examples of electron temperature profiles for a two-temperature ADAF. Here, βB = 0.5, Λi = 0, α = 0.1, γad = 5/3, and ro = 105rs. The curves correspond to different values of log10( f ): −4 (full), −5 (dotted), −6 (dashed), −7 (dot–dashed), and −8 (chain dot–dashed).
the electrons were assumed to be in isentropic balance so that the left-hand side of (1.23) was set to zero.
The existence of a two-temperature ADAF solution now depends on the Coulomb coupling timescale compared to the accretion timescale. A detailed calculation shows that as long as f < 0.3α2, a two-temperature ADAF solution exists. Representive profiles for Te are shown in figure 1.1 with α = 0.1. For this plot, the assumption that α << 1 has been relaxed. Also, radiation pressure and the optical depth are assumed to be negligible. The cooling function for the electrons includes magnetic bremsstrahlung, thermal bremsstrahlung (both electron-electron and electron-ion), and line cooling but not inverse Compton scattering. For large accretion rates, the last could result in significant cooling within <10 rs (Mahadevan 1997). For comparison, the ion temperature goes as r−1 and Ti  1010 K at r = 100 rs. The flow is subsonic everywhere with a Mach number of ∼0.07; for comparison, the Keplerian has a Mach number of ∼0.5. Thus, both models have implicitly assumed that the flow goes supersonic infinitesmally close to the event horizon. More advanced numerical ADAF models have addressed this issue with more appropriate inner boundary conditions (Narayan et al 1997, Gammie and Popham 1998).
1010 K at r = 100 rs. The flow is subsonic everywhere with a Mach number of ∼0.07; for comparison, the Keplerian has a Mach number of ∼0.5. Thus, both models have implicitly assumed that the flow goes supersonic infinitesmally close to the event horizon. More advanced numerical ADAF models have addressed this issue with more appropriate inner boundary conditions (Narayan et al 1997, Gammie and Popham 1998).
Since the gas flow in an ADAF is fairly similar to the Keplerian flow, the prescription for determining the spectrum detailed

Figure 1.2. Example spectrum for a two-temperature ADAF accretion model for Sgr A* using the profiles shown in figure 1.1. Here we use representative values of α = 0.3 and f = 10−4. The flow is inclined 60o to the line of sight.
Can be used if one assumes the ions play no role in the emission. The resulting spectrum for α = 0.3 and f = 10−4 is given in figure 1.2. The accretion rate for this model is ˙M = 4×1020 g s−1, much larger than the accretion rate used in the Keplerian model which produces the spectrum. The lower electron temperature results in less magnetic bremsstrahlung (even though the magnetic field for an ADAF is stronger since it is tied to the high-temperature ions). Also, for this representative case, the X-ray spectrum due to thermal bremsstrahlung from large radii is somewhat higher than the observations and in any case does not match the spectral index. We have ignored the fact that the magnetic field in an ADAF is assumed to be purely tangled while the field in the Keplerian flow is assumed to be purely azimuthal; the same magnetic bremsstrahlung emissivity has been used.
Comments on ADAFs
Except for the requirement that there be a large amount of angular momentum in the accreting gas, the properties of the flow at infinity have little impact on the structure and spectrum of ADAFs, making for very straightforward modeling. With fixed ion-electron coupling and viscosity, the primary free parameter is the mass accretion rate. The flow is purely determined by shear viscosity. In fact, it is explicitly assumed that viscosity is important, or else vr → 0 and no accretion occurs. Also, it has been pointed out (Narayan and Yi 1995a) that the Bernoulli parameter of ADAFs is positive, meaning that the gas has positive energy at infinity. Thus, it is possible that ADAFs occur in conjunction with some sort of outflow.
Both the Keplerian model and the ADAF model presented here do not satisfy general relativistic inner boundary conditions. For example, since a black hole cannot support shear stress, the torque at the event horizon must be zero (Gammie and Popham 1998). And although the spectral calculations might be general relativistic, the dynamical equations for both models are not. Calculations using pseudo-Newtonian gravity so that Φ = −GM/(r −rs) and Ω2 = GM/(r (r −rs)) have been done for ADAFs (Narayan et al 1997, Chen et al 1997) even in a Kerr metric where the black hole is no longer assumed to be non-rotating (Gammie and Popham 1998). Deviations within ∼5 rs are significant but do not appear to change the resulting spectrum substantially.
The condition that Γ >> Λ, it is seen that the entropy of the accreting gas in an ADAF increases as it falls inward. Thus, according to the Schwarzschild condition, ADAFs are unstable to convection (Narayan et al 2000). Calculations of ADAFs which include hydrothermal convection (Quataert and Gruzinov 2000) show that angular momentum is transported inward, resulting in a flatter density profile (ρ ∝ r−1/2) (CDAFs, convection dominated accretion flows). However, while some MHD calculations confirm this (Igumenshchev and Narayan 2002), others show that in the presence of turbulent magnetic fields, the net result of convection is to transport angular momentum outward (Hawley et al 2001). So although it is not certain what the effect of convection is when both resistive and viscous heating are present, it does appear that ADAF models which include convection without a more complete handling of the magnetic field are not self-consistent (Balbus and Hawley 2002).
A fundamental assumption of two-temperature ADAFs is that viscous heating followed by rapid accretion leads to a decoupling of the ions from the electrons. Although it has been shown that the Coulomb coupling itself may be too weak to maintain a thermal equilibrium, other mechanisms may prevent the formation of a two-temperature plasma. For example, Alfvenic turbulence or plasma waves in the presence of a magnetic field in thermal equipartition preferentially heats the electrons (Begelman and Chiueh 1988, Quataert and Gruzinov 1999). If such turbulence is due to collisionless shocks, the resulting heating rate will exceed the Coulomb rate, Γie, if M > 3×104 Mּ (Narayan and Yi 1995b). Thus, although ADAFs may be applicable to XRBs, for Sgr A*, where M = 2.6 × 106 Mּ, it is not at all clear that a stable large-scale two-temperature plasma develops.
 الاكثر قراءة في الثقوب السوداء
الاكثر قراءة في الثقوب السوداء
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















