Plotting Radioactive Decay
It is useful to plot the activity of a nuclide as it changes over time. Plots of this type can be used to determine when the activity will fall below a certain level. This plot is usually done showing activity on either a linear or a logarithmic scale. The decay of the activity of a single nuclide on a logarithmic scale will plot as a straight line because the decay is exponential.

Plotting the data points calculated above on both linear and semilog scales results in the graphs shown in Figure 1.

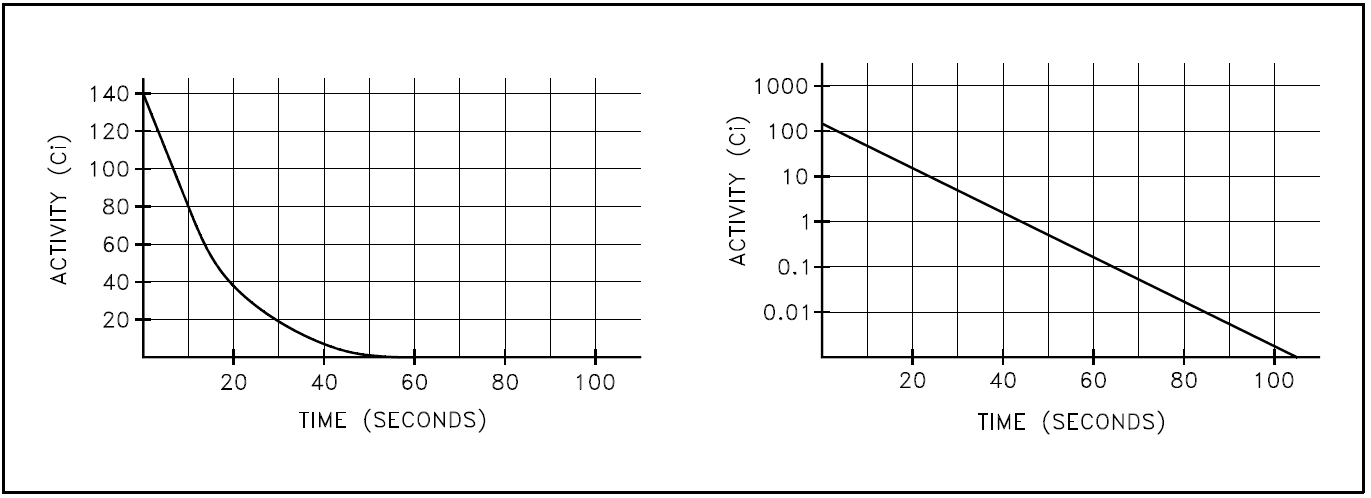
Figure 1: Linear and Semi-log Plots of Nitrogen-16 Decay

If a substance contains more than one radioactive nuclide, the total activity is the sum of the individual activities of each nuclide. As an example, consider a sample of material that contained 1 x 10⁶ atoms of iron-59 that has a half-life of 44.51 days (λ = 1.80 x 10^-7 sec^-1 ), 1 x 10⁶ atoms of manganese-54 that has a half-life of 312.2 days (λ = 2.57 x 10^-8 sec^-1), and 1 x 10⁶ atoms of cobalt-60 that has a half-life of 1925 days (λ = 4.17 x 10^-9 sec^-1). The initial activity of each of the nuclides would be the product of the number of atoms and the decay constant.

Plotting the manner in which the activities of each of the three nuclides decay over time demonstrates that initially the activity of the shortest-lived nuclide (iron-59) dominates the total activity, then manganese-54 dominates. After almost all of the iron and manganese have decayed away, the only contributor to activity will be the cobalt-60. A plot of this combined decay is shown in Figure 2.

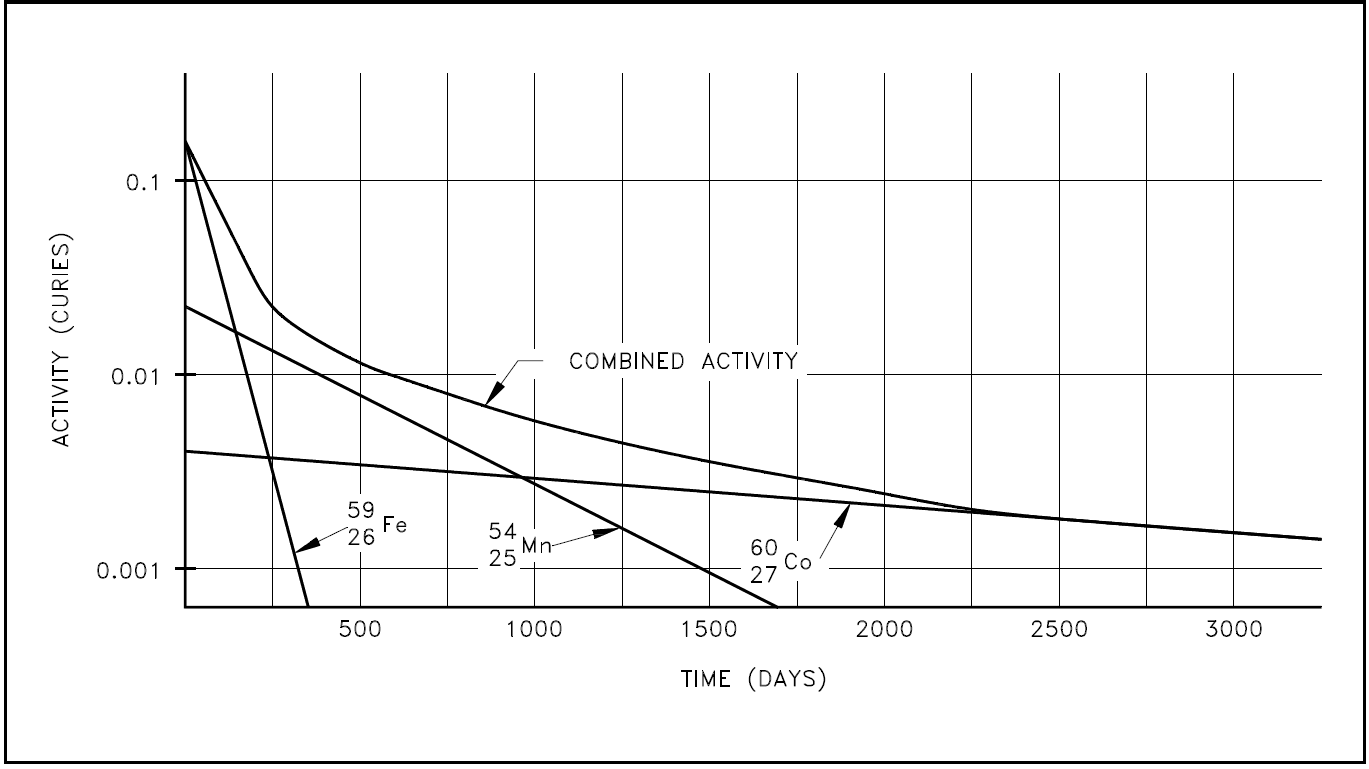
Figure 2: Combined Decay of Iron-56, Manganese-54, and Cobalt-60

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم الإعلام يشارك في الاجتماع التحضيري لمناقشة الخطة الإعلامية لزيارة عاشوراء

بحضور متوليها الشرعي.. العتبة العباسية المقدسة تواصل إقامة المجالس الحسينية لإحياء شهر المحرم

قسم الشؤون الفكرية يطلق برنامجه التبليغي في أكثر من 20 دولة إفريقية

شعبتا الخطابة النسوية والتوجيه الديني تواصلان إقامة المجالس الحسينية في مرقد أبي الفضل العباس (عليه السلام)

المزيد

الآخبار الصحية

دراسة تكشف علاقة خطيرة بين عمر الأم وصحة مولودها

دراسة تحذر.. اضطراب نوم بسيط قد يسبب الموت المبكر ؟

الاستحمام بالماء الساخن.. راحة مؤقتة وأضرار دائمة للبشرة

ماذا يحدث للجسم عند تخطي وجبة الإفطار؟

المزيد

الآخبار التكنلوجية

كيف تساعد الصيانة الوقائية في الحفاظ على كفاءة التكييف في سيارتك ؟

في ظاهرة غريبة حيرت العلماء.. كوكبنا قد يسجل أقصر يوم في التاريخ هذا الصيف!

السد الصيني العملاق يعيق دوران الأرض ويغيّر شكلها ؟

السعودية تطلق 10 تجارب علمية إلى محطة الفضاء الدولية

المزيد

مواضيع ذات صلة

مكشافات التأين الغازية

مكشافات الأشعة السينية

الكشف عن الأشعة السينية

علاقة المادة بالإشعاع

الأشعة السينية

تأثيرات الغلاف الجوي كجسم انتقائي الامتصاص للطاقة الإشعاعية

الأجسام انتقائية الامتصاص (Selective Obsorbing Bodies)

قوانين الاشعاع (Radiation Laws)

وحدات قياس الطاقة الحرارية الإشعاعية وطرق انتقالها وعملية عمليات الإشعاع ونقل الطاقة الحرارية وتبادلها.

الإشعاع وامتصاص الطاقة الاشعاعية

الأفلام الحساسة

النشاط الإشعاعي الصناعي والانشطار النووي