
Radioactive Equilibrium
 المؤلف:
U.S. Department of Commerce, National Technical Information Service, 1993
المؤلف:
U.S. Department of Commerce, National Technical Information Service, 1993
 المصدر:
The Nuclear Physics and Reactor Theory Handbook
المصدر:
The Nuclear Physics and Reactor Theory Handbook
 الجزء والصفحة:
p 38
الجزء والصفحة:
p 38
 29-3-2017
29-3-2017
 1952
1952
Radioactive Equilibrium
Radioactive equilibrium exists when a radioactive nuclide is decaying at the same rate at which it is being produced. Since the production rate and decay rate are equal, the number of atoms present remains constant over time.
An example of radioactive equilibrium is the concentration of sodium-24 in the coolant circulating through a sodium-cooled nuclear reactor. Assume that the sodium-24 is being produced at a rate of 1 x 10 atoms 6 per second. If the sodium-24 were stable and did not decay, the amount of sodium-24 present after some period of time could be calculated by multiplying the production rate by the amount of time. Plotting the amount of material present would result in the graph in Figure 1.
However, sodium-24 is not stable, and it decays with a half-life of 14.96 hours. If no sodium-24 is present initially and production starts at a rate of 1 x 106 atoms per second, the rate of decay will initially be zero because there is no sodium-24 present to decay. The rate of decay of sodium-24 will increase as the amount of sodium-24 increases.
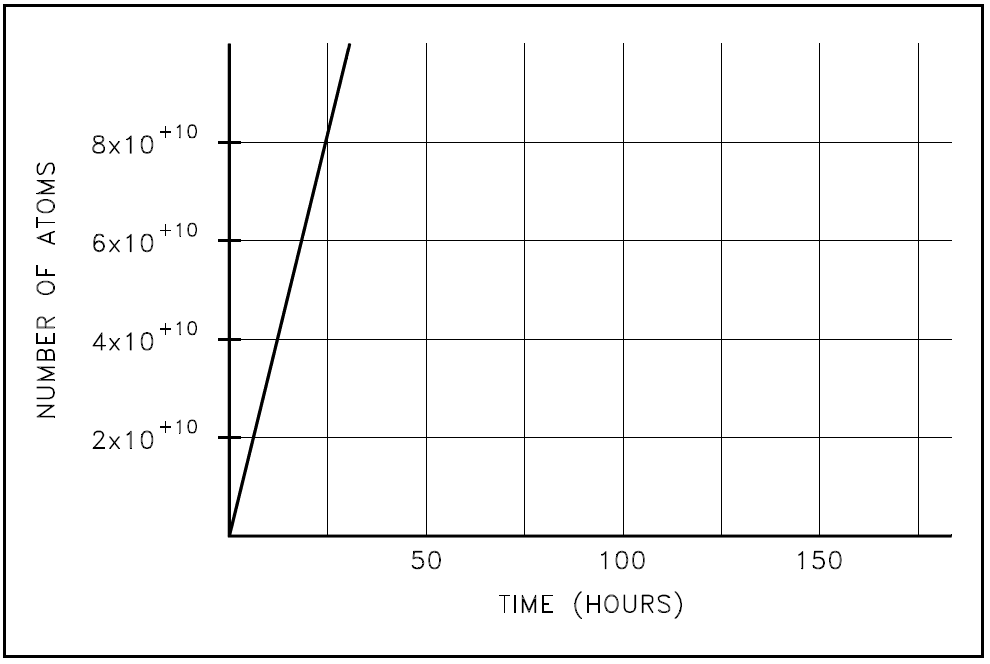
Figure 1: Cumulative Production of Sodium-24 Over Time
The amount of sodium-24 present will initially increase rapidly, then it will increase at a continually decreasing rate until the rate of decay is equal to the rate of production. It is possible to calculate how much sodium-24 will be present at equilibrium by setting the production rate (R) equal to the decay rate (λ N).
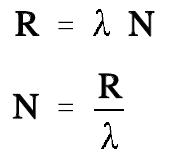
where:
R = production rate (atoms/second)
λ = decay constant (second-1)
N = number of atoms
It is possible to calculate the equilibrium value for sodium-24 being produced at a rate of 1 x 106 atoms/second.

The development of the equation to calculate how the amount of sodium-24 changes over time as it approaches the equilibrium value is beyond the scope of this handbook. However, the equation is presented below.
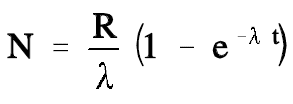
This equation can be used to calculate the values of the amount of sodium-24 present at different times. As the time increases, the exponential term approaches zero, and the number of atoms present will approach R/λ. A plot of the approach of sodium-24 to equilibrium is shown in Figure 2.
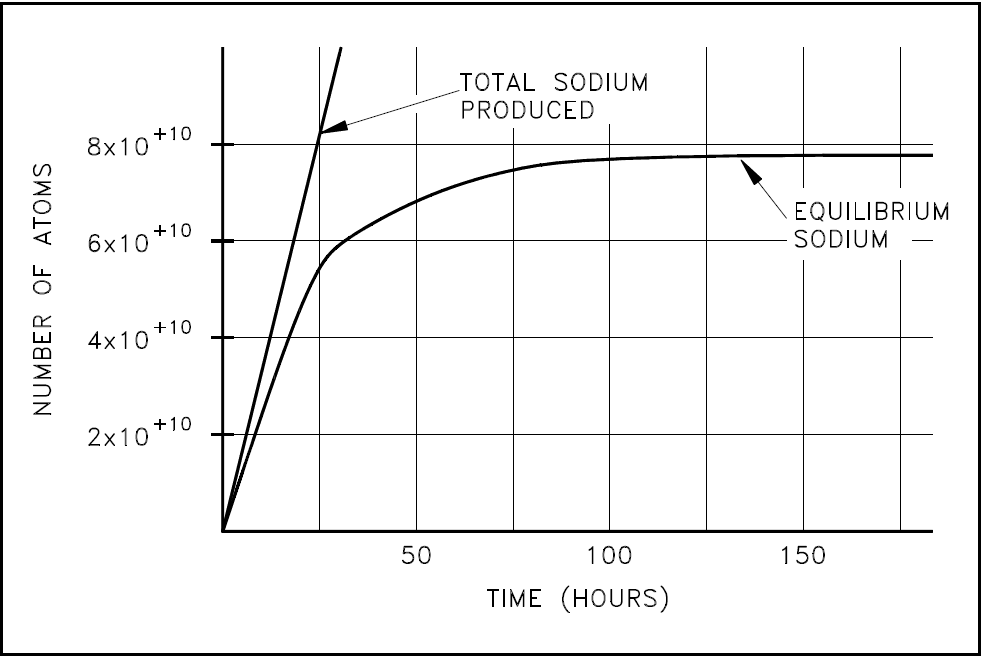
Figure 2: Approach of Sodium-24 to Equilibrium
 الاكثر قراءة في النشاط الاشعاعي
الاكثر قراءة في النشاط الاشعاعي
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


