
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Formation of Energy Bands
المؤلف:
Donald A. Neamen
المصدر:
Semiconductor Physics and Devices
الجزء والصفحة:
p 57
14-5-2017
5676
Formation of Energy Bands
Figure 1.la shows the radial probability density function for the lowest electron energy state of the single, noninteracting hydrogen atom, and Figure 1.lb shows the same probability curves for two atoms that are in close proximity to each other. The wave functions of the two atom electrons overlap, which means that the two electrons
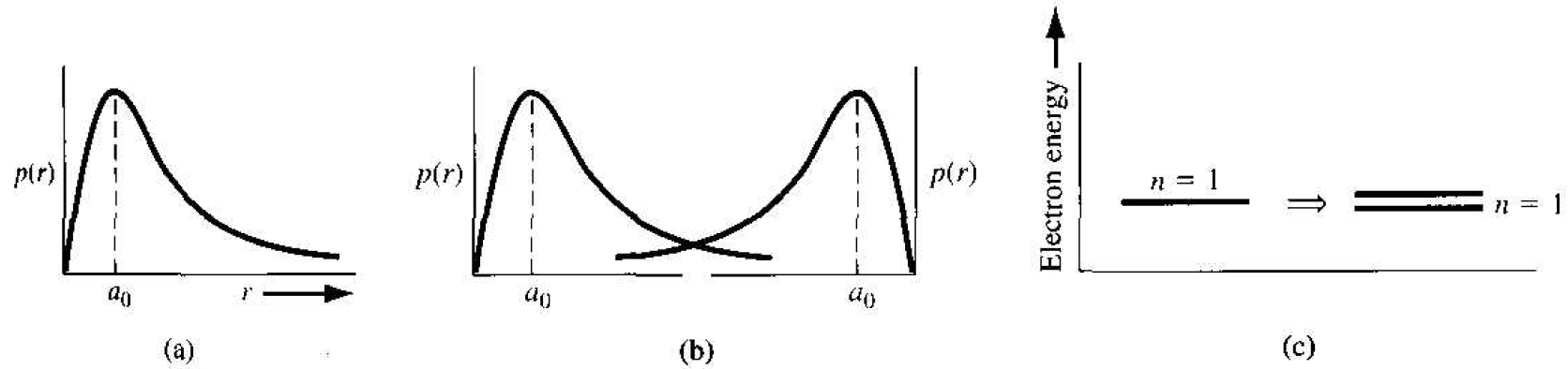
Figure 1.1 (a) Probability density function of an isolated hydrogen atom. (b) Overlapping probability density functions of two adjacent hydrogen atoms. (c) The splitting of the n = 1 state.
will interact. This interaction or perturbation results in the discrete quantized energy level splitting into two discrete energy levels, schematically shown in Figure 1.1c. The splitting of the discrete state into two states is consistent with the Pauli exclusion principle.
A simple analogy of the splitting of energy levels by interacting particles is the following. Two identical race cars and drivers are far apart on a race track. There is no interaction between the cars, so they both must provide the same power to achieve a given speed. However, if one car pulls up close behind the other car, there is an interaction called draft. The second car will be pulled to an extent by the lead car. The lead car will therefore require more power to achieve the same speed, since it is pulling the second car and the second car will require less power since it is being pulled by the lead car. So there is a "splitting" of power (energy) of the two interacting race cars. (Keep in mind not to take analogies too literally.)
Now, if we somehow start with a regular periodic arrangement of hydrogen type atoms that are initially very far apart, and begin pushing the atoms together, the initial quantized energy level will split into a band of discrete energy levels. This effect is shown schematically in Figure 1.2, where the parameter r0 represents the equilibrium interatomic distance in the crystal. At the equilibrium interatomic distance, there is a band of allowed energies, but within the allowed band, the energies are at discrete levels. The Pauli exclusion principle states that the joining of atoms to form a system (crystal) does not alter the total number of quantum states regardless of size. However, since no two electrons can have the same quantum number. the discrete energy must split into a band of energies in order that each electron can occupy a distinct quantum state.
We have seen previously that, at any energy level, the number of allowed quantum states is relatively small. In order to accommodate all of the electrons in a crystal, then, we must have many energy levels within the allowed hand. As an example, suppose that we have a system with 1019 one-electron atoms and also suppose that, at the equilibrium interatomic distance, the width of the allowed energy band is 1 eV. For simplicity, we assume that each electron in the system occupies a different energy level and, if the discrete energy states are equidistant, then the energy levels ate separated by l0-19 eV. This energy difference is extremely small, so that for all practical purposes, we have a quasi-continuous energy distribution through the allowed

Figure 1.2 The splitting of an energy state into a band of allowed energies.
energy band. The fact that 10-19 eV is a very small defference between two energy states can be seen from the following example.
Consider again a regular periodic arrangement of atoms, in which each atom now contains more than one electron. Suppose the atom in this imaginary crystal contains electrons up through the n = 3 energy level. If the atoms are initially very far apart, the electrons in adjacent atoms will not interact and will occupy the discrete energy levels. If these atoms are brought closer together, the outermost electrons in the n = 3 energy shell will begin to interact initially, so that this discrete energy level will split into a band of allowed energies. If the atoms continue to move closer together, the electrons in the n = 2 shell may begin to interact and will also split into a band of allowed energies. Finally, if the atoms become sufficiently close together, the innermost electrons in the n = 1 level may interact. so that this energy level may also split into a band of allowed energies. The splitting of these discrete energy levels is
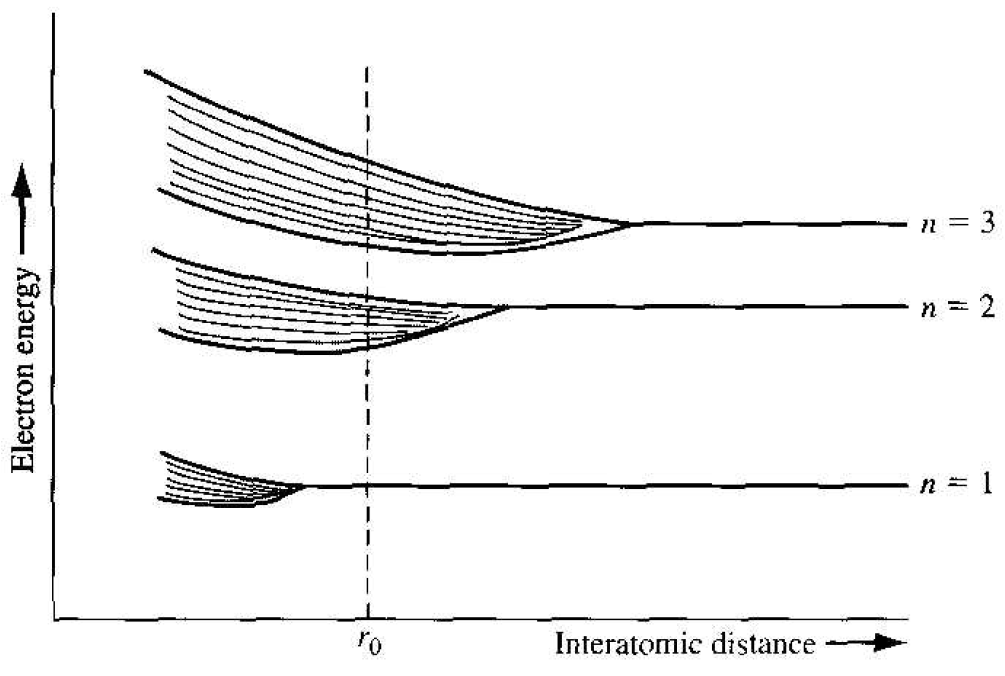
Figure 1.3 Schematic showing the splitting of three energy states into allowed hands of energies.

Figure 1.4 (a) Schematic of an isolated silicon atom. (b) The splitting of the 3s and 3p states of silicon into the allowed and forbidden energy bands.
qualitatively shown in Figure 1.3, If the equilibrium interatomic distance is r0. Then we have bands of allowed energies that the electrons may occupy separated by bands of forbidden energies. This energy-band splitting and the formation of allowed and forbidden bands is the energy-band theory of single-crystal materials.
The actual hand splitting in a crystal is much more complicated than indicated in Figure 1.3. A schematic representation of an isolated silicon atom is shown in Figure 1.4a. Ten of the fourteen silicon atom electrons occupy deep-lying energy levels close to the nucleus. The four remaining valence electrons are relatively weakly bound and are the electrons involved in chemical reactions. Figure 1.4b shows the hand splitting of silicon. We need only consider the n = 3 level for the valence electrons, since the first two energy shells are completely full and are tightly bound to the nucleus. The 3s state corresponds to n = 3 and I = 0 and contains two quantum states per atom. This state will contain two electrons at T = 0 K. The 3p state corresponds to n = 3 and l = 1 and contains six quantum states per atom. This state will contain the remaining two electrons in the individual silicon atom.
As the interatomic distance decreases, the 3s and 3p states interact and overlap. At the equilibrium interatomic distance, the bands have again split. hut now four quantum states per atom are in the lower hand and four quantum states per atom are in the upper hand. At absolute zero degrees, electrons are in the lowest energy state, so that all states in the lower band (the valence hand) will he full and all states in the upper band (the conduction band) will be empty. The handgap energy Eg between the top of the valence hand and the bottom of the conduction hand is the width of the forbidden energy band.
We have discussed qualitatively how and why bands of allowed and forbidden energies are formed in a crystal. The formation of these energy bands is directly related to the electrical characteristics of the crystal, as we will see later in our discussion.
 الاكثر قراءة في مواضيع عامة في الفيزياء الصلبة
الاكثر قراءة في مواضيع عامة في الفيزياء الصلبة
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















