Equilibrium Electron and Hole Concentrations

Figure 1.1 shows the energy-band diagram of a semiconductor when both donor and acceptor impurity atoms are added to the same region to form a compensated

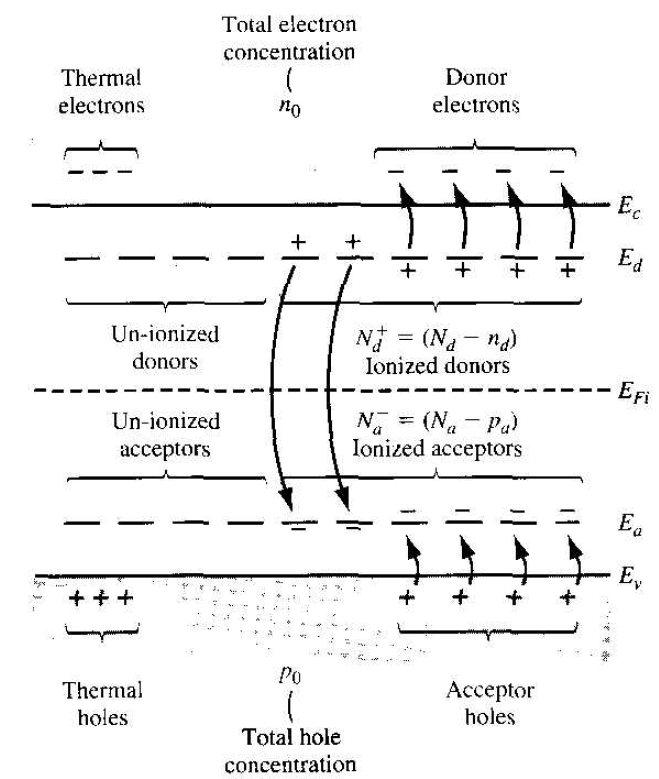
Figure 1.1 Energy-band diagram of a compensated semiconductor showing ionized and un-ionized donors and acceptors.

semiconductor. The figure shows how the electrons and holes can be distributed among the various states.

The charge neutrality condition is expressed by equating the density of negative charges to the density of positive charges. We then have

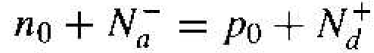(1)

or

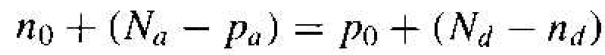(2)

where n₀ and p₀ are the thermal-equilibrium concentrations of electrons and holes in the conduction band and valence band, respectively. The parameter n_d is the concentration of electrons in the donor energy states, so N⁺_d = N_d – n_d is the concentration of positively charged donor states. Similarly, p_a is the concentration of holes in the and temperature. acceptor states, so N^-_a = N_a – p_a is the concentration of negatively charged acceptor states. We have expressions for n₀, p₀, n_d, and p_a in terms of the Fermi energy and temperature.

If we assume complete ionization, n,, and p, are both zero, and Equation (2) becomes

(3)

If we express p₀ as n²_i /n₀, then Equation (3) can be written as

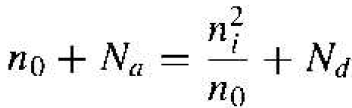(4a)

which in turn can be written as

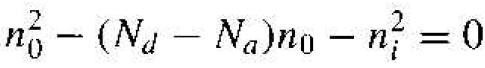(4b)

The electron concentration n_a can be determined using the quadratic formula, or

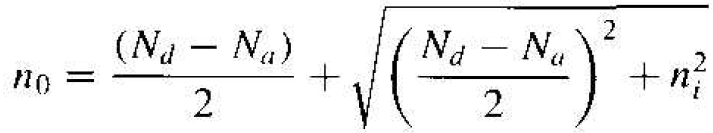(5)

The positive sign in the quadratic formula must he used, since, in the limit of an intrinsic semiconductor when N_a = N_d = 0. the electron concentration must be a positive quantity, or n₀ = n_i.

Equation (5) is used to calculate the electron concentration in an n-type semiconductor, or when N_d > N_a. Although Equation (5) was derived for a compensated semiconductor, the equation is also valid for N_a = 0.

اخر الاخبار

اخبار العتبة العباسية المقدسة

خمسون عامًا من العطاء.. نجم الأعرجي خادم الزائرين بلا انقطاع

العتبة العباسية المقدسة تواصل إقامة مجالسها العزائية لإحياء شهر المحرم

العتبة العباسية المقدسة تطلق سلسلة محاضرات قرآنية عاشورائية في بابل

في مساء اليوم الخامس من المحرّم.. المواكب الكربلائيّة تواصل فعالياتها العزائية

المزيد

الآخبار الصحية

لهذا السبب.. إغلاق 25 مركزًا لعلاج الإدمان في مصر ؟

خلافا للاعتقاد الشائع.. علماء يكشفون أسرار بذور البطيخ ؟!

هذا ما يحدث لجسمك عند تناولك الطماطم بانتظام !

تعرف على أطعمة تسرّع "تعافي الجسم" من حروق الشمس

المزيد

الآخبار التكنلوجية

الثلوج تغطي الصحراء الأكثر جفافا في العالم!

بتلسكوب "ألما".. التقاط صورا غير مسبوقة لبدايات الكون !

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

المزيد

مواضيع ذات صلة

( قليل من التحذيرات) الغشاء المطاطي لا يكفي: تحذيرات لفهم الزمكان المعوج

حركي KINETIC

حساسية الوسيلة (الآلة) INSTRUMENT SENSITIVITY

مقدمة في البنية الذرية

نماذج فریدمان

التلسكوبات الراديوية

تيار النزف BLEEDING CURRENT

"الميكانيكا الكمية والتجريبية المنطقية: رؤية كاسيرر للنظريات الفيزيائية"

أدنى مواصفات MINIMUM SPECIFICATIONS

كم يجب أن تكون عليه كتلة الكون؟

الحجم النووي Nuclean Size

ربوتات النانو (Nanorobots)