Mathematical Derivation

The position of the Fermi energy level within the bandgap can be determined by using the equations already developed for the thermal-equilibrium electron and hole concentrations. If we assume the Boltzmann approximation to be valid,  we have n₀ = N_c exp[-(E_c – E_F)/kT].

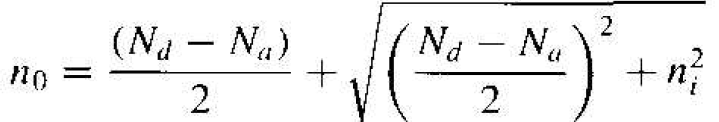(1)

We can solve for E_c - E_F from this equation and obtain

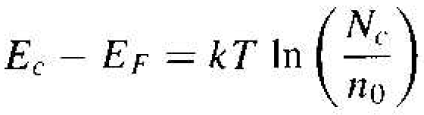(2)

where n₀ is given by Equation (1). If we consider an n-type semiconductor in which N_d >> n_i, then n₀ ≈ N_d, so that

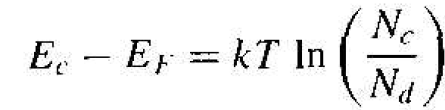(3)

The distance between the bottom of the conduction band and the Fermi energy is a logarithmic function of the donor concentration. As the donor concentration increases, the Fermi level moves closer to the conduction band. Conversely, if the Femi level moves closer to the conduction band, then the electron concentration in the conduction band is increasing. We may note that if we have a compensated semiconductor, then the N_d term in Equation (3) is simply replaced by N_d – N_a, or the net effective donor concentration. We may develop a slightly different expression for the position of the Fermi level. That n₀ = n_i exp[(E_F - E_Fi)/kT]. We can solve for E_F - E_Fi as

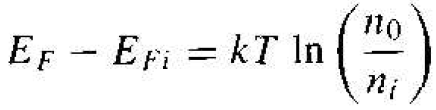(4)

Equation (4) can be used specifically for an n-type semiconductor, where n₀ is given by Equation (1). to find the difference between the Fermi level and the intrinsic Fermi level as a function of the donor concentration. We may note that, if the net effective donor concentration is zero, that is, N_d – N_a = 0, then n₀ = n_i and E_F = E_Fi. A completely compensated semiconductor has the characteristics of an intrinsic material in terms of carrier concentration and Fermi level position.

We can derive the same types of equations for a p-type semiconductor.  We have p₀ = N_v  exp [-(E_F – E_v)/kT]. so that

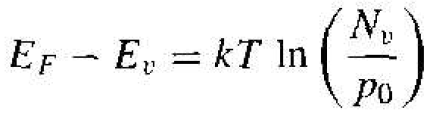(5)

If we assume that N_a  >> n_i. then Equation (5) can be written as

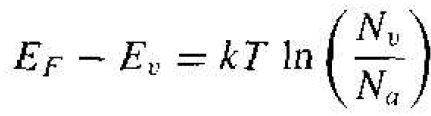(6)

The distance between the Fermi level and the top of the valence-band energy for a p-type semiconductor is a logarithmic function or the acceptor concentration: as the acceptor concentration increases, the Fermi level moves closer to the valence band. Equation (6) still assumes that the Boltzmann approximation is valid. Again. if we have a compensated p-type semiconductor, then the N_a term in Equation (6) is replaced by N_a - N_d, or the net effective acceptor concentration.

We can also derive an expression for the relationship between the Fermi level and the intrinsic Fermi level in terms of the hole concentration. We have  that p₀ = n_i exp [-(E_F - E_Fi )/kT]. which yields

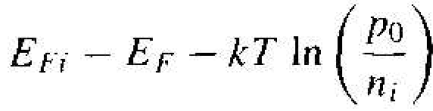(7)

Equation (7) can be used to find the difference between the intrinsic Fermi level and the Fermi energy in terms of the acceptor concentration. The hole concentration p₀ in Equation (7). We may again note from Equation (4) that, for an n-type semiconductor, n₀ > n_i and E_F > E_Fi. The Fermi level for an n-type semiconductor is above E_Fi. For a p-type semiconductor, p₀ > n_i , and from Equation (7) we see that

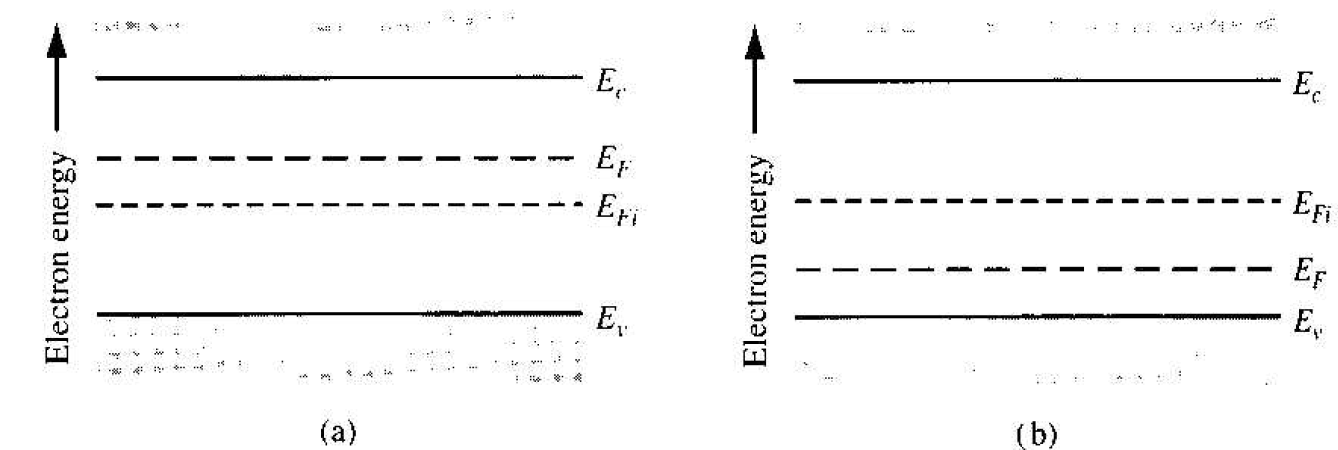
Figure 1.1 1 Position of Fermi level for an (a) n-type (N_d > N_a) and (b) p-type (N_d > N_a) semiconductor.

E_Fi > E_F. The Fermi level for a p-type semiconductor is below E_Fi. These result are shown in Figure 1.1.