
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Complete Ionization and Freeze-Out
المؤلف:
Donald A. Neamen
المصدر:
Semiconductor Physics and Devices
الجزء والصفحة:
p 129
18-5-2017
5778
Complete Ionization and Freeze-Out
The probability function for electrons in the donor energy state was just given by Equation (1).
 (1)
(1)
If we assume that (Ed - EF) >> kT, then
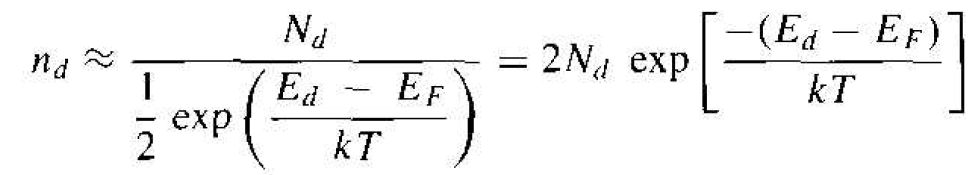 (2)
(2)
If (Ed – EF) >> kT, then the Boltzmann approximation is also valid for the electrons in the conduction band so that
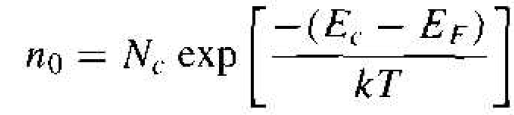
We can determine the relative number of electrons in the donor state company with the total number of electrons; therefore we can consider the ratio of electrons the donor state to the total number of electrons in the conduction band plus dose state. Using the expressions of Equations (2), we write
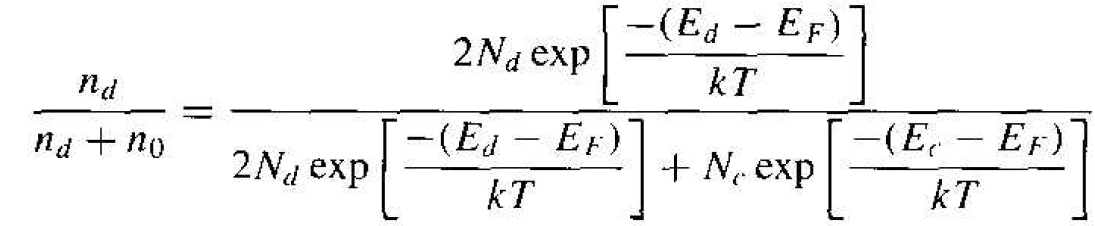 (3)
(3)
The Fermi energy cancels out of this expression. Dividing by the numerator term, we obtain
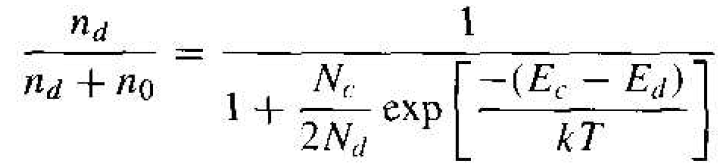 (4)
(4)
The factor (Ec – Ed) is just the ionization energy of the donor electrons.
At room temperature, then, the donor states are essentially completely ionized and, for a typical doping of 1016 cm-3, almost all donor impurity atoms have donated an electron to the conduction band.
At room temperature, there is also essentially complete ionization of the acceptor atoms. This means that each acceptor atom has accepted an electron from the valence band so that pa is zero. At typical acceptor doping concentrations, a hole is created in the valence hand for each acceptor atom. This ionization effect and the creation of electrons and holes in the conduction band and valence band, respectively, are shown in Figure 1.1.
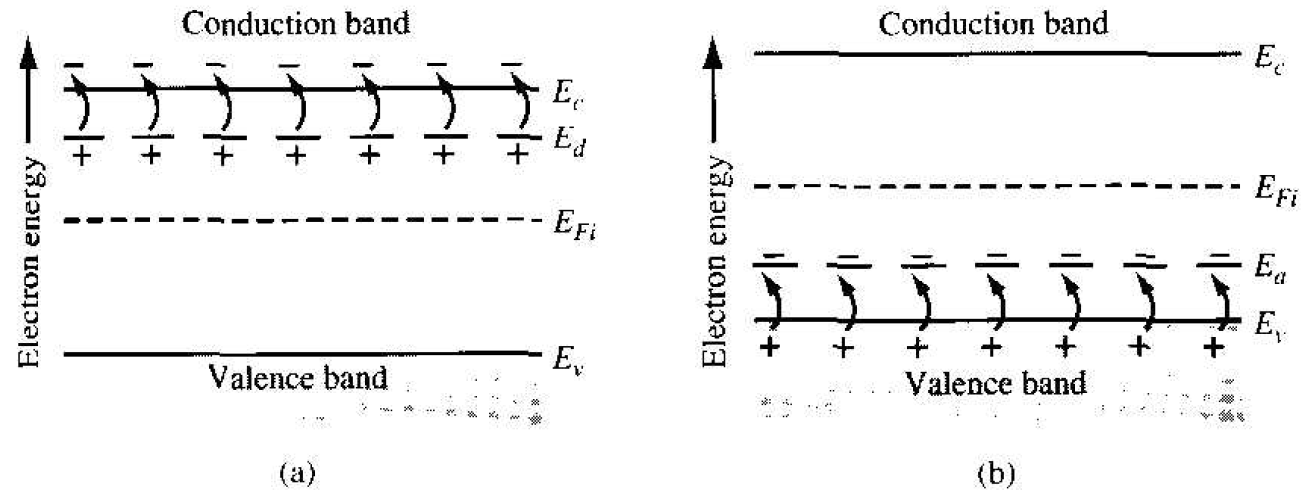
Figure 1.1 Energy-hand diagrams showing complete ionization of (a) donor states and (b) acceptor states.
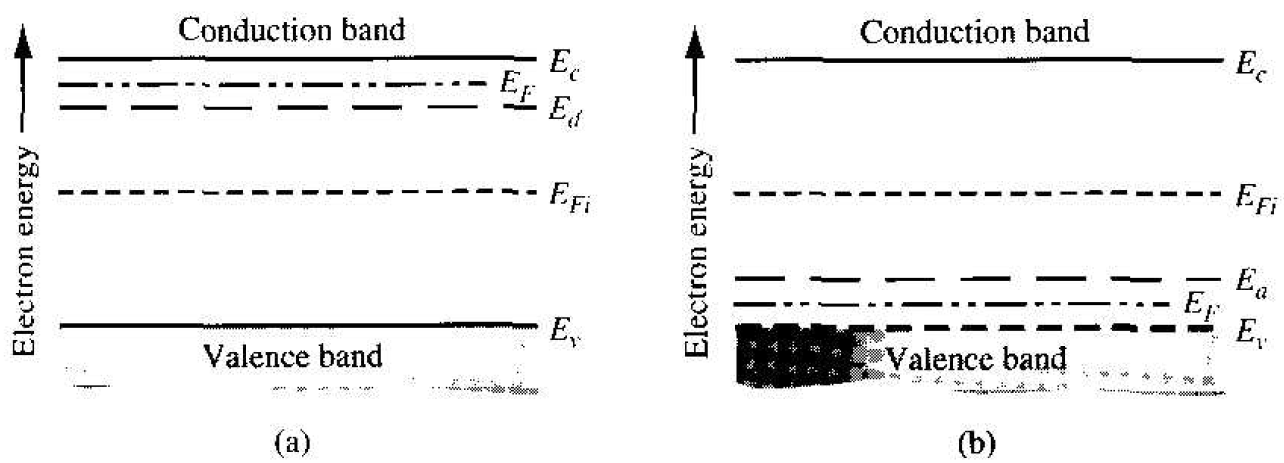
Figure 1.2 Energy-band diagram at T = 0 K for (a) n-type and (b) p-type semiconductors.
The opposite of complete ionization occurs at T = 0 K. At absolute zero degrees, all electrons are in their lowest possible energy state; that is, for an n-type semiconductor, each donor state must contain an electron, therefore nd = Nd or N+d = 0. We must have, then, from Equation (1) that exp [ (Ed – EF) / kT] = 0. Since T = 0 K, this will occur for exp (-∞) = 0, which means that EF > Ed. The Fermi energy level must be above the donor energy level at absolute zero. In the case of a p-type semiconductor at absolute zero temperature, the impurity atoms will not contain any electrons, so that the Fermi energy level must be below the acceptor energy state. The distribution of electrons among the various energy states, and hence the Fermi energy, is a function of temperature.
A detailed analysis, not given in this text, shows that at T = 0 K, the Fermi energy is halfway between Ec and Ed for the n-type material and halfway between Ea and Ev for the p-type material. Figure 1.2 shows these effects. No electrons from the donor state are thermally elevated into the conduction band; this effect is called freeze-out. Similarly, when no electrons from the valance band are elevated into the acceptor states, the effect is also called freeze-out.
 الاكثر قراءة في مواضيع عامة في الفيزياء الصلبة
الاكثر قراءة في مواضيع عامة في الفيزياء الصلبة
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















