تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
زاوية بروستر Brewster Angle
المؤلف:
محمد عطية سويلم، د. محمد روبين إدريس، بديع صالح الخطيب، د. أحمد يوسف قواسمة
المصدر:
الفيزياء العامة
الجزء والصفحة:
ص 307
1-12-2019
9596
زاوية بروستر Brewster's Angle
إن الضوء عبارة عن أمواج كهرومغناطيسية ، أي أن هناك مجالا كهربائيا متذبذبا ، ويتذبذب معه وعموميا عليه مجال مغناطيسي ، وكلاهما عمودي على اتجاه انتشار الموجة ، واذا أخذنا موجة واحدة في أثناء انتشارها أمكن ان نعين اتجاها لتذبذب لهذه الموجة ، وهذا الاتجاه والذي هو الطبع عمودي على اتجاه الانتشار سيكون - أي اتجاه التذبذب - باتجاه محصلة المجال الكهربائي والمجال المغناطيسي ، وفي هذه الحالة نقول ان الضوء مستقطب خطياً .
ولو كان البحث يقتصر على موجة واحدة لهذا الأمر ، إلا انه في الأحوال العادية ، ينطلق من مصادر الضوء ملايين الملايين من الموجات وكل منها مستقطبة في اتجاه معين ، لذا فإن الضوء ، المنطق منها غير مستقطب لأن اتجاه الاهتزاز عشوائي .
ويمكن تبسيط الأمر بتحليل كل متجه كهرمغناطيسي لموجة إلى مركبتين في اتجاهين ، نقوم نحن باختيارها . وبالطبع ، لا بد أن يكونا معامدين لاتجاه الانتشار ، عندئذ سنحصل على ضوء غير مستقطب ، إلا انه واضح المركبات . وبالطبع ستكون المركبات متساويتين في الاتساع .
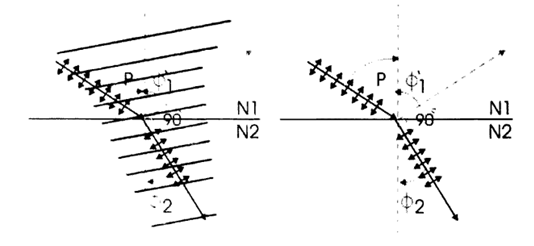
الشكل (1)
وقد وجد ان الضوء عندما يسقط من وسط شفاف على سطح وسط شفاف أخر . فإن الجزء المنعكس والجزء المنكسر يختلفان في حالة الاستقطاب ، ولتوضيح ذلك انظر إلى الشكل (1) الذي يبين أشعة ضوئية غير مستقطبة تسقط على سطح مادة شفافة (ماء أو زجاج مثلا) ، بزاوية قدرها (1Φ) ، فينعكس جزء منها بزارية (1Φ`) وينكسر جزء منها بزاوية (2Φ) . نلاحظ أننا حللنا المتجه الكهرمغناطيسي للموجة الساقطة إلى مركبتين ، الأولى عمودية على الصفحة . وسنسميها المركبة العمودية ، والثانية في مستوى الصفحة ، وسنسميها المركبة الموازية .
إن الموجات الضوئية المنعكسة تكون فيها المركبة العمودية أكبر مقدارا من المركبة الموازية . وخلافا للضوء المنكسر ، فإن المركبة الموازية تكون اكبر من المعامدة .
وقد وجد تجريبيا انه عند زاوية سقوط معينة ، تسمى زاوية الاستقطاب ، تتلاشى المركبة الموازية من الموجات الضوئية المنعكسة يكون الضوء المنعكس عند هذه الزاوية خطيا ، وفي اتجاه عمودي على سطح الانعكاس (وهو السطح الذي يجمع الشعاع الساقط والمنعكس والعمود المقام من نقطة السقوط) . اما اذا نظرنا للضوء المنكسر فسنجد أن المركبة المعامدة قد تلاشت ، وأن الضوء المنكسر مستقطب خطيا في اتجاه يوازي سطح الانعكاس انظر الشكل (1) .
كما وجد تجريبيا انه عند زاوية الاستقطاب ، يكون الشعاع المنكسر عموديا على الشعاع المنعكس ، أي أن :
= 90Φ`1 + Φ2
وقد سميت زاوية الاستقطاب بزاوية بروستر نسبة إلى العالم الذي اكتشفها ويرمز لها بالرمز (pΦ) . ويمكننا ايجاد علاقة لزاوية بروستر كما يلي :
لأن 
قانون سنل 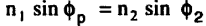
وبما أن جا الزاوية = جتا المتممة لها ، إذن :