A Chaitin's constant, also called a Chaitin omega number, introduced by Chaitin (1975), is the halting probability of a universal prefix-free (self-delimiting) Turing machine. Every Chaitin constant is simultaneously computably enumerable (the limit of a computable, increasing, converging sequence of rationals), and algorithmically random (its binary expansion is an algorithmic random sequence), hence uncomputable (Chaitin 1975).

A Chaitin's constant can therefore be defined as

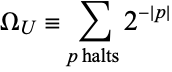(1)

which gives the probability that for any set of instructions, a particular prefix-free universal Turing machine will halt, where 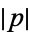 is the size in bits of program .

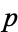The value of a Chaitin constant is highly machine-dependent. In some cases, it can even be proved that not a single bit can be computed (Solovay 2000).

Chaitin constants 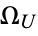 are perhaps the most obvious specific example of uncomputable numbers. They are also known to be transcendental.

Calude et al. (2002) computed the first 64 bits of Chaitin's constant 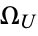 for a certain universal Turing machine as

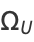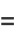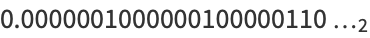			(2)
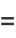			(3)

(OEIS A079365 and A100264).

Calude and Dinneen (2007) subsequently computed the first 43 and 40 bits of another prefix-free Turing machine which is universal when used with data in base 16 and 2, respectively, as

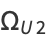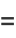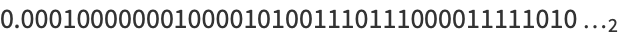			(4)
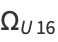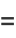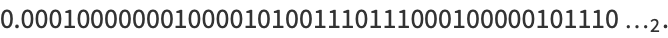			(5)

The binary result is engraved on the medallion presented to Gregory Chaitin for his 60th birthday by Stephen Wolfram, illustrated above.

REFERENCES:

Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, p. 145, 2003.

Calude, C. S.; Dinneen, M. J.; and Shu, C.-K. "Computing a Glimpse of Randomness." Exper. Math. 11, 361-370, 2002.

Calude, C. S. and Dinneen, M. J. "Exact Approximations of Omega Numbers." Int. J. Bifur. Chaos 17, 1937-1954, 2007.

Chaitin, G. J. "A Theory of Program Size Formally Identical to Information Theory." J. Assoc. Comput. Mach. 22, 329-340, 1975.

Chaitin, G. J. "How Much Information Can There be in a Real Number?" Int. J. Bifur. Chaos 17, 1933-1935, 2007.

Chaitin, G. Meta Math!:The Quest for Omega. New York: Pantheon Books, 2005.

Finch, S. R. "Chaitin's Constant." §1.11 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 81-83, 2003.

Gardner, M. "The Random Number 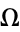 Bids Fair to Hold the Mysteries of the Universe." Sci. Amer. 241, 20-34, Nov. 1979.

Gardner, M. "Chaitin's Omega." Ch. 21 in Fractal Music, Hypercards, and More Mathematical Recreations from Scientific American Magazine. New York: W. H. Freeman, pp. 307-319, 1992.

Kobayashi, K. "Sigma(N)O-Complete Properties of Programs and Lartin-Lof Randomness." Information Proc. Let. 46, 37-42, 1993.

Sloane, N. J. A. Sequences A079365 and A100264 in "The On-Line Encyclopedia of Integer Sequences."

Solovay, R. M. "A Version of 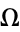 for Which ZFC Cannot Predict a Single Bit." In Finite Versus Infinite. Contributions to an Eternal Dilemma (Ed. C. Calude and G. Păun). London: Springer-Verlag, pp. 323-334, 2000.