

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Transcendental Number
المؤلف:
Allouche, J.-P. and Cosnard, M
المصدر:
"The Komornik-Loreti Constant Is Transcendental." Amer. Math. Monthly 107
الجزء والصفحة:
...
3-2-2021
5441
Transcendental Number
A transcendental number is a (possibly complex) number that is not the root of any integer polynomial, meaning that it is not an algebraic number of any degree. Every real transcendental number must also be irrational, since a rational number is, by definition, an algebraic number of degree one.
A complex number 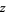 can be tested to see if it is transcendental using the Wolfram Language command Not[Element[x, Algebraics]].
can be tested to see if it is transcendental using the Wolfram Language command Not[Element[x, Algebraics]].
Transcendental numbers are important in the history of mathematics because their investigation provided the first proof that circle squaring, one of the geometric problems of antiquity that had baffled mathematicians for more than 2000 years was, in fact, insoluble. Specifically, in order for a number to be produced by a geometric construction using the ancient Greek rules, it must be either rational or a very special kind of algebraic number known as a Euclidean number. Because the number 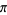 is transcendental, the construction cannot be done according to the Greek rules.
is transcendental, the construction cannot be done according to the Greek rules.
Liouville showed how to construct special cases (such as Liouville's constant) using Liouville's approximation theorem. In particular, he showed that any number that has a rapidly converging sequence of rational approximations must be transcendental. For many years, it was only known how to determine if special classes of numbers were transcendental. The determination of the status of more general numbers was considered an important enough unsolved problem that it was one of Hilbert's problems.
Great progress was subsequently made by Gelfond's theorem, which gives a general rule for determining if special cases of numbers of the form 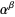 are transcendental. Baker produced a further revolution by proving the transcendence of sums of numbers of the form
are transcendental. Baker produced a further revolution by proving the transcendence of sums of numbers of the form 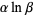 for algebraic numbers
for algebraic numbers 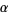 and
and 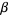 .
.
The number e was proven to be transcendental by Hermite in 1873, and pi (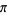 ) by Lindemann in 1882. Gelfond's constant
) by Lindemann in 1882. Gelfond's constant 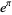 is transcendental by Gelfond's theorem since
is transcendental by Gelfond's theorem since
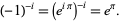 |
The Gelfond-Schneider constant 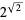 is also transcendental (Hardy and Wright 1979, p. 162).
is also transcendental (Hardy and Wright 1979, p. 162).
Known transcendentals are summarized in the following table, where 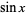 is the sine function,
is the sine function, 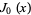 is a Bessel function of the first kind,
is a Bessel function of the first kind, 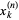 is the
is the 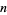 th zero of
th zero of 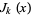 ,
, 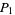 is the Thue-Morse constant,
is the Thue-Morse constant, 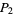 is the universal parabolic constant,
is the universal parabolic constant, 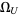 is Chaitin's constant,
is Chaitin's constant, 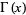 is the gamma function, and
is the gamma function, and 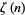 is the Riemann zeta function.
is the Riemann zeta function.
| transcendental number | reference |
Chaitin's constant 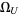 |
|
| Champernowne constant | |
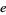 |
Hermite (1873) |
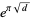 , , 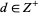 |
Nesterenko (1999) |
Gelfond's constant 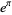 |
Gelfond |
Gelfond-Schneider constant 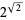 |
Hardy and Wright (1979, p. 162) |
exponential factorial inverse sum 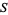 |
J. Sondow, pers. comm., Jan. 10, 2003 |
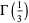 |
Le Lionnais (1983, p. 46) |
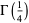 |
Chudnovsky (1984, p. 308), Waldschmidt, Nesterenko (1999) |
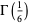 |
Chudnovsky (1984, p. 308) |
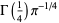 |
Davis (1959) |
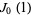 |
Hardy and Wright (1979, p. 162) |
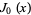 smallest root, 2.4048255... smallest root, 2.4048255... |
Le Lionnais (1983, p. 46) |
| Komornik-Loreti constant | Allouche and Cosnard (2000) |
Liouville's constant 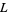 |
Liouville (1850) |
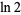 |
Hardy and Wright (1979, p. 162) |
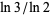 |
Hardy and Wright (1979, p. 162), |
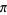 |
Lindemann (1882) |
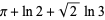 |
Borwein et al. (1989) |
Plouffe's constant 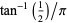 |
Smith 2003, Margolius |
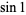 |
Hardy and Wright (1979, p. 162) |
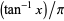 for for  rational and rational and 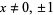 |
Margolius |
| Thue-Morse constant 0.4124540336... | Dekking (1977), Allouche and Shallit |
| Thue constant | |
universal parabolic constant 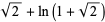 |
Apéry's constant 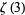 has been proved to be irrational, but it is not known if it is transcendental. At least one of
has been proved to be irrational, but it is not known if it is transcendental. At least one of 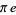 and
and 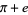 (and probably both) are transcendental, but transcendence has not been proven for either number on its own. It is not known if
(and probably both) are transcendental, but transcendence has not been proven for either number on its own. It is not known if 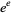 ,
, 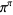 ,
, 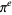 ,
, 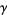 (the Euler-Mascheroni constant),
(the Euler-Mascheroni constant), 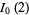 , or
, or 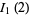 (where
(where 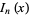 is a modified Bessel function of the first kind) are transcendental.
is a modified Bessel function of the first kind) are transcendental.
There are still many fundamental and outstanding problems in transcendental number theory, including the constant problem and Schanuel's conjecture.
REFERENCES:
Allouche, J. P. and Shallit, J. In preparation.
Allouche, J.-P. and Cosnard, M. "The Komornik-Loreti Constant Is Transcendental." Amer. Math. Monthly 107, 448-449, 2000.
Bailey, D. H. and Crandall, R. E. "Random Generators and Normal Numbers." Exper. Math. 11, 527-546, 2002.
Baker, A. "Approximations to the Logarithm of Certain Rational Numbers." Acta Arith. 10, 315-323, 1964.
Baker, A. "Linear Forms in the Logarithms of Algebraic Numbers I." Mathematika 13, 204-216, 1966.
Baker, A. "Linear Forms in the Logarithms of Algebraic Numbers II." Mathematika 14, 102-107, 1966.
Baker, A. "Linear Forms in the Logarithms of Algebraic Numbers III." Mathematika 14, 220-228, 1966.
Baker, A. "Linear Forms in the Logarithms of Algebraic Numbers IV." Mathematika 15, 204-216, 1966.
Borwein, J. M.; Borwein, P. B.; and Bailey, D. H. "Ramanujan, Modular Equations, and Approximations to Pi or How to Compute One Billion Digits of Pi." Amer. Math. Monthly 96, 201-219, 1989.
Chudnovsky, G. V. Contributions to the Theory of Transcendental Numbers. Providence, RI: Amer. Math. Soc., 1984.
Courant, R. and Robbins, H. "Algebraic and Transcendental Numbers." §2.6 in What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 103-107, 1996.
Davis, P. J. "Leonhard Euler's Integral: A Historical Profile of the Gamma Function." Amer. Math. Monthly 66, 849-869, 1959.
Dekking, F. M. "Transcendence du nombre de Thue-Morse." C. R. Acad. Sci. Paris 285, 157-160, 1977.
Gourdon, X. and Sebah, P. "Transcendental Numbers." §3 in "Classification of Numbers: Overview." https://numbers.computation.free.fr/Constants/Miscellaneous/classification.html.
Gray, R. "Georg Cantor and Transcendental Numbers." Amer. Math. Monthly 101, 819-832, 1994.
Hardy, G. H. and Wright, E. M. "Algebraic and Transcendental Numbers," "The Existence of Transcendental Numbers," and "Liouville's Theorem and the Construction of Transcendental Numbers." §11.5-11.6 in An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Oxford University Press, pp. 159-164, 1979.
Hermite, C. "Sur la fonction exponentielle." C. R. Acad. Sci. Paris 77, 18-24, 74-79, and 226-233, 1873.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 46, 1979.
Lindemann, F. "Über die Zahl 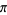 ." Math. Ann. 20, 213-225, 1882.
." Math. Ann. 20, 213-225, 1882.
Liouville, J. "Sur des classes très-étendues de quantités dont la valeur n'est ni algébrique, ni même réductible à des irrationelles algébriques." J. Math. pures appl. 15, 133-142, 1850.
Margolius, B. H. "Plouffe's Constant Is Transcendental." https://www.lacim.uqam.ca/~plouffe/articles/plouffe.pdf.
Nagell, T. Introduction to Number Theory. New York: Wiley, p. 35, 1951.
Nesterenko, Yu. V. "On Algebraic Independence of the Components of Solutions of a System of Linear Differential Equations." Izv. Akad. Nauk SSSR, Ser. Mat. 38, 495-512, 1974. English translation in Math. USSR 8, 501-518, 1974.
Nesterenko, Yu. V. "Modular Functions and Transcendence Questions." [Russian.] Mat. Sbornik 187, 65-96, 1996. English translation in Sbornik Math. 187, 1319-1348, 1996.
Nesterenko, Yu. V. A Course on Algebraic Independence: Lectures at IHP 1999. Unpublished manuscript. 1999.
Pickover, C. A. "The Fifteen Most Famous Transcendental Numbers." J. Recr. Math. 25, 12, 1993.
Ramachandra, K. Lectures on Transcendental Numbers. Madras, India: Ramanujan Institute, 1969.
Shidlovskii, A. B. Transcendental Numbers. New York: de Gruyter, 1989.
Siegel, C. L. Transcendental Numbers. New York: Chelsea, 1965.
Smith, W. D. "Pythagorean Triples, Rational Angles, and Space-Filling Simplices." 2003. https://math.temple.edu/~wds/homepage/diophant.pdf.
Tijdeman, R. "An Auxiliary Result in the Theory of Transcendental Numbers." J. Numb. Th. 5, 80-94, 1973.
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















