A constant, sometimes also called a "mathematical constant," is any well-defined real number which is significantly interesting in some way. In this work, the term "constant" is generally reserved for real nonintegral numbers of interest, while "number" is used to refer to interesting integers (e.g., Brun's constant, but beast number). However, in contexts such as linear combination, the term "constant" is generally used to mean "scalar" or "real number," and need not exclude integer values.

A function, equation, etc., is said to "be constant" (or be a constant function) if it always assumes the same value independent of how its parameters are varied.

Certain constants are known to many decimal digits and recur throughout many diverse areas of mathematics, often in unexpected and surprising places (e.g., pi, e, and to some extent, the Euler-Mascheroni constant 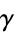). Other constants are more specialized and may be known to only a few digits. S. Plouffe maintains a site about the computation and identification of numerical constants. Plouffe's site also contains a page giving the largest number of digits computed for the most common constants. S. Finch maintains a delightful, more expository site containing detailed essays and references on constants both common and obscure.

The mathematician Glaisher remarked, "No doubt the desire to obtain the values of these quantities to a great many figures is also partly due to the fact that most of them are interesting in themselves; for 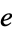, , 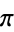, , 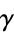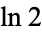and many other numerical quantities occupy a curious, and some of them almost a mysterious, place in mathematics, so that there is a natural tendency to do all that can be done towards their precise determination" (Gourdon and Sebah).

The following table lists some common constants, their symbols, and approximate values.

constant	Wolfram Language	symbol	OEIS	approx. value
Apéry's constant	Zeta[3]		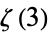A002117	1.20206...
Catalan's constant	Catalan		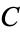A006752	0.915966...
Delian constant	2^(1/3)		A002580	1.25992...
e	E		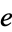A001113	2.71828...
Euler-Mascheroni constant	EulerGamma		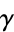A001620	0.577216...
Glaisher-Kinkelin constant	Glaisher		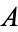A074962	1.28243...
golden ratio	GoldenRatio		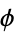A001622	1.61803...
Khinchin's constant	Khinchin		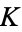A002210	2.68545...
natural logarithm of 2	Log[2]		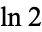A002162	0.693147...
pi	Pi		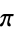A000796	3.14159...
Pythagoras's constant	Sqrt[2]		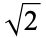A002193	1.41421...
Soldner's constant		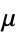	A070769	1.45136...

Gourdon and Sebah and Lyster maintain web pages comparing the fastest known algorithms for computing digits of common constants.

REFERENCES:

Bailey, D. H. and Crandall, R. E. "On the Random Character of Fundamental Constant Expansions." Exper. Math. 10, 175-190, 2001. http://www.nersc.gov/~dhbailey/dhbpapers/baicran.pdf.

Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, p. 145, 2003.

Borwein, J. and Borwein, P. A Dictionary of Real Numbers. London: Chapman & Hall, 1990.

Finch, S. R. Mathematical Constants. Cambridge, England: Cambridge University Press, 2003.

Gourdon, X. and Sebah, P. "Numbers, Constants and Computation." http://numbers.computation.free.fr/Constants/constants.html.

Gourdon, X. and Sebah, P. "User Constants (Compute log(2), zeta(3), Catalan Constant, Pi with Arctan Formulas ... with pifast." http://numbers.computation.free.fr/Constants/PiProgram/userconstants.html.

Gourdon, X. and Sebah, P. "Constants and Records of Computation." http://numbers.computation.free.fr/Constants/Miscellaneous/Records.html.

Kondo, S. "PI WORLD OF JA0HXV." http://ja0hxv.calico.jp/pai/estart.html.

Le Lionnais, F. Les nombres remarquables. Paris: Hermann, 1983.

Lyster, S. "Stu's Pi Page: The Fastest Pi Programs on the Planet." http://home.istar.ca/~lyster/otherconstants.html.

Michon, G. P. "Final Answers: Numerical Constants." http://home.att.net/~numericana/answer/constants.htm.

Munafo, R. "Notable Properties of Specific Numbers." http://home.earthlink.net/~mrob/pub/math/numbers.html.

Niklasch, G. "Some Number-Theoretical Constants Arising as Products of Rational Functions of 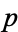 over the Primes." http://www.gn-50uma.de/alula/essays/Moree/Moree.en.shtml.

Plouffe, S. "Plouffe's Inverter." http://pi.lacim.uqam.ca/eng/.

Plouffe, S. "Plouffe's Inverter: Table of Current Records for the Computation of Constants." http://pi.lacim.uqam.ca/eng/records_en.html.

Plouffe, S. "Miscellaneous Mathematical Constants." http://www.worldwideschool.org/library/books/sci/math/MiscellaneousMathematicalConstants/toc.html.

Robinson, H. P. and Potter, E. Mathematical Constants. Report UCRL-20418. Berkeley, CA: University of California, 1971.

Trott, M. "Mathematical Constants." §2.2.4 in The Mathematica GuideBook for Programming. New York: Springer-Verlag, pp. 171-180, 2004. http://www.mathematicaguidebooks.org/.

Wells, D. W. The Penguin Dictionary of Curious and Interesting Numbers. Harmondsworth, England: Penguin Books, 1986.