

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Continued Fraction Constants
المؤلف:
Borwein, J.; Bailey, D.; and Girgensohn, R.
المصدر:
Experimentation in Mathematics: Computational Paths to Discovery. Wellesley, MA: A K Peters
الجزء والصفحة:
...
28-4-2020
720
A number of closed-form constants can be obtained for generalized continued fractions having particularly simple partial numerators and denominators.
The Ramanujan continued fractions provide a fascinating class of continued fraction constants. The Trott constants are unexpected constants whose partial numerators and denominators correspond to their decimal digits (though to achieve this, it is necessary to allow some partial numerators to equal 0).
The first in a series of other famous continued fraction constants is the infinite regular continued fraction
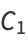 |
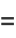 |
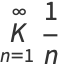 |
(1) |
 |
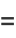 |
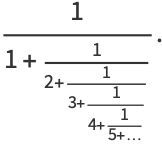 |
(2) |
The first few convergents 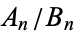 of the constant are 0, 1, 2/3, 7/10, 30/43, 157/225, 972/1393, 6961/9976, ... (OEIS A001053 and A001040).
of the constant are 0, 1, 2/3, 7/10, 30/43, 157/225, 972/1393, 6961/9976, ... (OEIS A001053 and A001040).
Both numerator 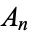 and denominator
and denominator 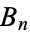 satisfy the recurrence relation
satisfy the recurrence relation
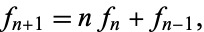 |
(3) |
where 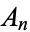 has the initial conditions
has the initial conditions 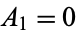 ,
, 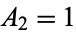 and
and 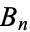 has the initial conditions
has the initial conditions 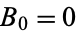 ,
, 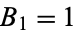 . These can be solved exactly to yield
. These can be solved exactly to yield
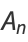 |
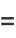 |
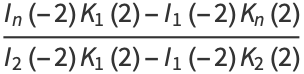 |
(4) |
 |
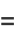 |
![2[(-1)^nI_n(2)K_1(2)+I_1(2)K_n(2)]](https://mathworld.wolfram.com/images/equations/ContinuedFractionConstants/Inline21.gif) |
(5) |
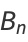 |
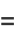 |
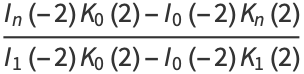 |
(6) |
 |
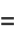 |
![2[(-1)^(n-1)I_n(2)K_0(2)+I_0(2)K_n(2)],](https://mathworld.wolfram.com/images/equations/ContinuedFractionConstants/Inline27.gif) |
(7) |
where 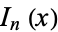 is a modified Bessel function of the first kind and
is a modified Bessel function of the first kind and 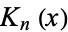 is a modified Bessel function of the second kind. Therefore, as
is a modified Bessel function of the second kind. Therefore, as 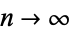 , the infinite continued fraction is given by
, the infinite continued fraction is given by
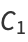 |
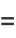 |
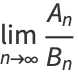 |
(8) |
 |
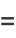 |
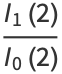 |
(9) |
 |
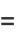 |
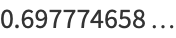 |
(10) |
(OEIS A052119; Lehmer 1973, Rabinowitz 1990; Borwein et al. 2004, p. 35).
The related constant defined by the generalized continued fraction
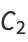 |
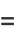 |
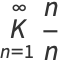 |
(11) |
 |
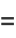 |
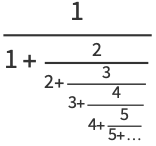 |
(12) |
has 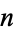 th convergent is given by
th convergent is given by
![(A_n)/(B_n)=[(Gamma(n+2))/(!(n+1))-1]^(-1),](https://mathworld.wolfram.com/images/equations/ContinuedFractionConstants/NumberedEquation2.gif) |
(13) |
where 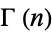 is the gamma function and
is the gamma function and 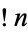 is the subfactorial. The first few convergents
is the subfactorial. The first few convergents 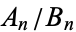 are therefore 1, 1/2, 3/5, 11/19, 53/91, 103/177, ... (OEIS A053557 and A103816). As
are therefore 1, 1/2, 3/5, 11/19, 53/91, 103/177, ... (OEIS A053557 and A103816). As 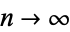 , this gives the value
, this gives the value
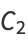 |
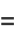 |
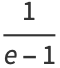 |
(14) |
 |
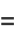 |
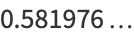 |
(15) |
(OEIS A073333).
Another similar continued fraction constant that can be computed in closed form is
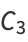 |
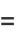 |
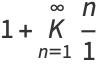 |
(16) |
 |
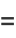 |
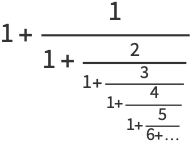 |
(17) |
 |
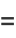 |
![sqrt(2/(epi))[erfc(2^(-1/2))]^(-1)](https://mathworld.wolfram.com/images/equations/ContinuedFractionConstants/Inline65.gif) |
(18) |
 |
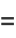 |
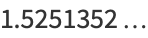 |
(19) |
(OEIS A111129), where erfc is the complementary error function. No closed form is known for the convergents, but for 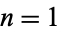 , 2, ..., the first few convergents are 1, 1/3, 2/3, 4/9, 7/12, 19/39, 68/123, ... (OEIS A225435 and A225436).
, 2, ..., the first few convergents are 1, 1/3, 2/3, 4/9, 7/12, 19/39, 68/123, ... (OEIS A225435 and A225436).
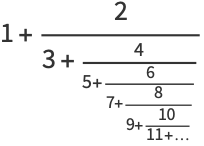
Another closed-form continued fraction is given by
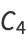 |
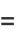 |
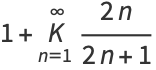 |
(20) |
 |
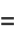 |
 |
(21) |
 |
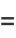 |
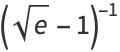 |
(22) |
 |
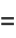 |
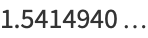 |
(23) |
(OEIS A113011). The first few convergents are 5/3, 29/19, 233/151, 2329/1511, 27949/18131, 78257/50767, ... (OEIS A113012 and A113013).
The general infinite continued fraction ![[b_0;b_1,b_2...]](https://mathworld.wolfram.com/images/equations/ContinuedFractionConstants/Inline82.gif) with partial quotients that are in arithmetic progression is given by
with partial quotients that are in arithmetic progression is given by
![[A+D,A+2D,A+3D,...]=(I_(A/D)(2/D))/(I_(1+A/D)(2/D))](https://mathworld.wolfram.com/images/equations/ContinuedFractionConstants/NumberedEquation3.gif) |
(24) |
(Schroeppel 1972) for real 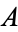 and
and 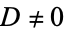 .
.
Perron (1954-57) discusses continued fractions having terms even more general than the arithmetic progression and relates them to various special functions. He does not, however, appear to specifically consider equation (24).
REFERENCES:
Borwein, J.; Bailey, D.; and Girgensohn, R. Experimentation in Mathematics: Computational Paths to Discovery. Wellesley, MA: A K Peters, pp. 34-35, 2004.
Finch, S. R. "Euler-Gompertz Constant." §6.2 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 423-428, 2003.
Guy, R. K. "Review: The Mathematics of Plato's Academy." Amer. Math. Monthly 97, 440-443, 1990.
Lehmer, D. H. "Continued Fractions Containing Arithmetic Progressions." Scripta Math. 29, 17-24, 1973.
Perron, O. Die Lehre von den Kettenbrüchen, 3. verb. und erweiterte Aufl. Stuttgart, Germany: Teubner, 1954-57.
Rabinowitz, S. Problem E3264. "Asymptotic Estimates from Convergents of a Continued Fraction." Amer. Math. Monthly 97, 157-159, 1990.
Schroeppel, R. Item 99 in Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, p. 36, Feb. 1972. https://www.inwap.com/pdp10/hbaker/hakmem/cf.html#item99.
Sloane, N. J. A. Sequences A001040/M2863, A001053/M1783, A052119, A053557, A073333, A103816, A111129, A113011, A113012, A113013, A225435, and A2225436 in "The On-Line Encyclopedia of Integer Sequences."