A number is said to be simply normal to base  if its base- expansion has each digit appearing with average frequency tending to .

A normal number is an irrational number for which any finite pattern of numbers occurs with the expected limiting frequency in the expansion in a given base (or all bases). For example, for a normal decimal number, each digit 0-9 would be expected to occur 1/10 of the time, each pair of digits 00-99 would be expected to occur 1/100 of the time, etc. A number that is normal in base- is often called -normal.

A number that is -normal for every , 3, ... is said to be absolutely normal (Bailey and Crandall 2003).

As stated by Kac (1959), "As is often the case, it is much easier to prove that an overwhelming majority of objects possess a certain property than to exhibit even one such object....It is quite difficult to exhibit a 'normal' number!" (Stoneham 1970).

If a real number  is -normal, then it is also -normal for  and  integers (Kuipers and Niederreiter 1974, p. 72; Bailey and Crandall 2001). Furthermore, if  and  are rational with  and  is -normal, then so is , while if  is an integer, then  is also -normal (Kuipers and Niederreiter 1974, p. 77; Bailey and Crandall 2001).

Determining if numbers are normal is an unresolved problem. It is not even known if fundamental mathematical constants such as pi (Wagon 1985, Bailey and Crandall 2003), the natural logarithm of 2  (Bailey and Crandall 2003), Apéry's constant  (Bailey and Crandall 2003), Pythagoras's constant  (Bailey and Crandall 2003), and e are normal, although the first 30 million digits of  are very uniformly distributed (Bailey 1988).

While tests of  for  (Pythagoras's constant digits, 3 (Theodorus's constant digits, 5, 6, 7, 8, 10, 11, 12, 13, 14, 15 indicate that these square roots may be normal (Beyer et al. 1970ab), normality of these numbers has (possibly until recently) also not been proven. Isaac (2005) recently published a preprint that purports to show that each number of the form  for  not a perfect square is simply normal to the base 2. Unfortunately, this work uses a nonstandard approach that appears rather cloudy to at least some experts who have looked at it.

While Borel (1909) proved the normality of almost all numbers with respect to Lebesgue measure, with the exception of a number of special classes of constants (e.g., Stoneham 1973, Korobov 1990, Bailey and Crandall 2003), the only numbers known to be normal (in certain bases) are artificially constructed ones such as the Champernowne constant and the Copeland-Erdős constant. In particular, the binary Champernowne constant

(1)

(OEIS A030190) is 2-normal (Bailey and Crandall 2001).

Bailey and Crandall (2001) showed that, subject to an unproven but reasonable hypothesis related to pseudorandom number generators, the constants , , and  would be 2-normal, where  is Apéry's constant. Stoneham (1973) proved that the so-called Stoneham numbers

(2)

where  and  are relatively prime positive integers, are -normal whenever  is an odd prime  and  is a primitive root of . This result was extended by Bailey and Crandall (2003), who showed that  is normal for all positive integers  provided only that  and  are relatively prime.

Korobov (1990) showed that the constants

(3)

are -normal for  positive integers and  and  relatively prime, a result reproved using completely different techniques by Bailey and Crandall (2003). Amazingly, Korobov (1990) also gave an explicit algorithm for computing terms in the continued fraction of .

Bailey and Crandall (2003) also established -normality for constants of the form  for certain sequences of integers  and .

REFERENCES:

Bailey, D. H. "The Computation of 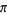 to 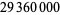 Decimal Digit using Borwein's' Quartically Convergent Algorithm." Math. Comput. 50, 283-296, 1988.

Bailey, D. H. and Crandall, R. E. "On the Random Character of Fundamental Constant Expansions." Exper. Math. 10, 175-190, 2001. https://www.nersc.gov/~dhbailey/dhbpapers/baicran.pdf.

Bailey, D. H. and Crandall, R. E. "Random Generators and Normal Numbers." Exper. Math. 11, 527-546, 2002.

Beyer, W. A.; Metropolis, N.; and Neergaard, J. R. "Square Roots of Integers 2 to 15 in Various Bases 2 to 10: 88062 Binary Digits or Equivalent." Math. Comput. 23, 679, 1969.

Beyer, W. A.; Metropolis, N.; and Neergaard, J. R. "Statistical Study of Digits of Some Square Roots of Integers in Various Bases." Math. Comput. 24, 455-473, 1970a.

Beyer, W. A.; Metropolis, N.; and Neergaard, J. R. "The Generalized Serial Test Applied to Expansions of Some Irrational Square Roots in Various Bases." Math. Comput. 24, 745-747, 1970b.

Borel, É. "Les probabilités dénombrables et leurs applications arithmétiques." Rend. Circ. Mat. Palermo 27, 247-271, 1909.

Champernowne, D. G. "The Construction of Decimals Normal in the Scale of Ten." J. London Math. Soc. 8, 254-260, 1933.

Copeland, A. H. and Erdős, P. "Note on Normal Numbers." Bull. Amer. Math. Soc. 52, 857-860, 1946.

Gibbs, W. W. "A Digital Slice of Pi. The New Way to do Pure Math: Experimentally." Sci. Amer. 288, 23-24, May 2003.

Good, I. "Normal Recurring Decimals." J. London Math. Soc. 21, 167-169, 1946.

Good, I. J. and Gover, T. N. "The Generalized Serial Test and the Binary Expansion of 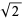." J. Roy. Statist. Soc. Ser. A 130, 102-107, 1967.

Good, I. J. and Gover, T. N. "Corrigendum." J. Roy. Statist. Soc. Ser. A 131, 434, 1968.

Isaac, R. "On the Simple Normality to Base 2 of 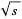, for 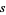 Not a Perfect Square." 16 Dec 2005. https://arxiv.org/abs/math.NT/0512404.

Kac, M. Statistical Independence in Probability, Analysis and Number Theory. Washington, DC: Math. Assoc. Amer., 1959.

Korobov, N. "Continued Fractions of Certain Normal Numbers." Math. Zametki 47, 28-33, 1990. English translation in Math. Notes Acad. Sci. USSR 47, 128-132, 1990.

Kuipers, L. and Niederreiter, H. Uniform Distribution of Sequences. New York: Wiley, 1974.

Postnikov, A. G. "Ergodic Problems in the Theory of Congruences and of Diophantine Approximations." Proc. Steklov Inst. Math. 82, 1966.

Sloane, N. J. A. Sequence A030190 in "The On-Line Encyclopedia of Integer Sequences."

Stoneham, R. "A General Arithmetic Construction of Transcendental Non-Liouville Normal Numbers from Rational Functions." Acta Arith. 16, 239-253, 1970. https://matwbn.icm.edu.pl/ksiazki/aa/aa16/aa1631.pdf.

Stoneham, R. "On Absolute 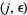-Normality in the Rational Fractions with Applications to Normal Numbers." Acta Arith. 22, 277-286, 1973. https://matwbn.icm.edu.pl/ksiazki/aa/aa16/aa1632.pdf.

Wagon, S. "Is 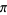 Normal?" Math. Intel. 7, 65-67, 1985.

Weisstein, E. W. "Bailey and Crandall Discover a New Class of Normal Numbers." MathWorld Headline News, Oct. 4, 2001. https://mathworld.wolfram.com/news/2001-10-04/normal/.

Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 26, 1986.