

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Equidistributed Sequence
المؤلف:
Hardy, G. H. and Littlewood, J. E.
المصدر:
"Some Problems of Diophantine Approximation." Acta Math. 37
الجزء والصفحة:
...
26-10-2020
1634
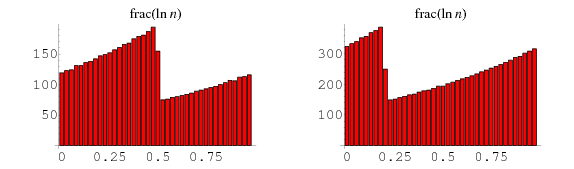
A sequence of real numbers {x_n}" src="https://mathworld.wolfram.com/images/equations/EquidistributedSequence/Inline1.gif" style="height:15px; width:23px" /> is equidistributed on an interval
![[a,b]](https://mathworld.wolfram.com/images/equations/EquidistributedSequence/Inline2.gif) if the probability of finding
if the probability of finding 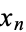 in any subinterval is proportional to the subinterval length. The points of an equidistributed sequence form a dense set on the interval
in any subinterval is proportional to the subinterval length. The points of an equidistributed sequence form a dense set on the interval ![[a,b]](https://mathworld.wolfram.com/images/equations/EquidistributedSequence/Inline4.gif) .
.
However, dense sets need not necessarily be equidistributed. For example, {frac(lnn)}_n" src="https://mathworld.wolfram.com/images/equations/EquidistributedSequence/Inline5.gif" style="height:15px; width:70px" />, where
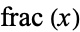 is the fractional part, is dense in
is the fractional part, is dense in ![[0,1]](https://mathworld.wolfram.com/images/equations/EquidistributedSequence/Inline7.gif) but not equidistributed, as illustrated above for
but not equidistributed, as illustrated above for 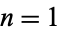 to 5000 (left) and
to 5000 (left) and 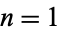 to
to 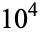 (right)
(right)
Hardy and Littlewood (1914) proved that the sequence {frac(x^n)}_n" src="https://mathworld.wolfram.com/images/equations/EquidistributedSequence/Inline11.gif" style="height:15px; width:62px" />, of power fractional parts is equidistributed for almost all real numbers
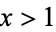 (i.e., the exceptional set has Lebesgue measure zero). Exceptional numbers include the positive integers, the silver ratio
(i.e., the exceptional set has Lebesgue measure zero). Exceptional numbers include the positive integers, the silver ratio 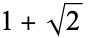 (Finch 2003), and the golden ratio
(Finch 2003), and the golden ratio 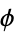 .
.
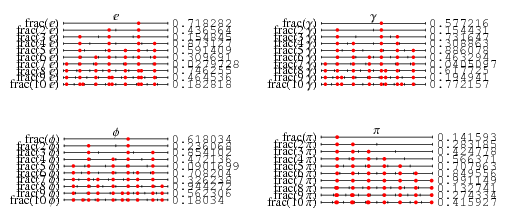
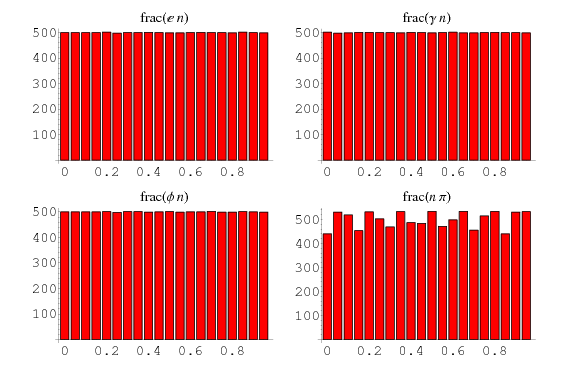
The top set of above plots show the values of {frac(kx)}_(k=0)^(10)" src="https://mathworld.wolfram.com/images/equations/EquidistributedSequence/Inline15.gif" style="height:19px; width:79px" /> for
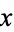 equal to e, the Euler-Mascheroni constant
equal to e, the Euler-Mascheroni constant 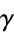 , the golden ratio
, the golden ratio 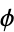 , and pi. Similarly, the bottom set of above plots show a histogram of the distribution of
, and pi. Similarly, the bottom set of above plots show a histogram of the distribution of {frac(kx)}_(k=0)^(10000)" src="https://mathworld.wolfram.com/images/equations/EquidistributedSequence/Inline19.gif" style="height:19px; width:87px" /> for these constants. Note that while most settle down to a uniform-appearing distribution,
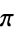 curiously appears nonuniform after
curiously appears nonuniform after 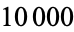 iterations. Steinhaus (1999) remarks that the highly uniform distribution of
iterations. Steinhaus (1999) remarks that the highly uniform distribution of 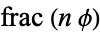 has its roots in the form of the continued fraction for
has its roots in the form of the continued fraction for 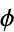 .
.
Now consider the number of empty intervals in the distribution of {frac(kx)}_(k=0)^n" src="https://mathworld.wolfram.com/images/equations/EquidistributedSequence/Inline24.gif" style="height:17px; width:79px" /> in the intervals bounded by the intervals determined by 0,
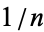 ,
, 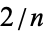 , ...,
, ..., 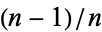 , 1 for
, 1 for 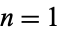 , 2, ..., summarized below for the constants previously considered.
, 2, ..., summarized below for the constants previously considered.
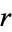 |
Sloane | # empty intervals for 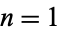 , 2, ... , 2, ... |
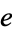 |
A036412 | 0, 0, 0, 0, 1, 0, 0, 1, 1, 3, 1, 4, 4, 7, 5, ... |
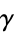 |
A046157 | 0, 0, 0, 1, 0, 0, 0, 1, 2, 2, 3, 0, 3, 5, 3, ... |
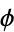 |
A036414 | 0, 0, 0, 0, 0, 0, 1, 0, 2, 0, 1, 1, 0, 2, 2, ... |
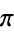 |
A036416 | 0, 1, 1, 1, 1, 0, 0, 1, 2, 3, 4, 4, 5, 7, 7, ... |
The values of 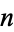 for which no bins are left blank are given in the following table.
for which no bins are left blank are given in the following table.
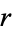 |
Sloane | 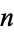 with no empty intervals with no empty intervals |
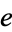 |
A036413 | 1, 2, 3, 4, 6, 7, 32, 35, 39, 71, 465, 536, 1001, ... |
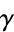 |
A046158 | 1, 2, 3, 5, 6, 7, 12, 19, 26, 97, 123, 149, 272, 395, ... |
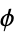 |
A036415 | 1, 2, 3, 4, 5, 6, 8, 10, 13, 16, 21, 34, 55, 89, 144, ... |
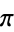 |
A036417 | 1, 6, 7, 106, 112, 113, 33102, 33215, ... |
REFERENCES:
Hardy, G. H. and Littlewood, J. E. "Some Problems of Diophantine Approximation." Acta Math. 37, 193-239, 1914.
Kuipers, L. and Niederreiter, H. Uniform Distribution of Sequences. New York: Wiley, 1974.
Pólya, G. and Szegö, G. Problems and Theorems in Analysis I. New York: Springer-Verlag, p. 88, 1972.
Sloane, N. J. A. Sequences A036412, A036413, A036414, A036415, A036416, A036417, A046157, and A046158 in "The On-Line Encyclopedia of Integer Sequences."
Vardi, I. Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, pp. 155-156, 1991.