Nuclear Magnetic Moments

Both the proton and neutron are spin 1/2 particles, which means that they each have a spin angular momentum with two allowed spin states, spin up and spin down. If you place either of these particles in a magnetic field, one of the projections will gain magnetic energy while the other loses it.
For an electron, the high magnetic energy state was when the spin pointed parallel to the magnetic field. Because the proton has the opposite charge from the electron, the opposite orientation is the high magnetic energy state.
If the Dirac equation is applied accurately to a proton, then the formula for the proton’s magnetic moment would be one nuclear magneton μ_N defined by the equation

which is the Bohr magneton formula with the electron mass replaced by the proton mass. Since the proton is 1836 times heavier than an electron, a nuclear magneton is 1/1836 times smaller than a Bohr magneton.
The Dirac equation, however, does not give the correct value for the proton’s magnetic moment μ_p . The experimental value is

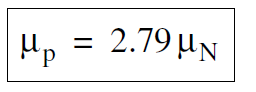
The fact that the Dirac equation is off by a factor of 2.79 is one indication that the proton is a more complex object than the electron. (The Dirac equation is not exact even for the electron.
The experimental value for the electron’s magnetic moment is 1.00114 Bohr magnetons. The correction of .00114 Bohr magnetons is accurately explained by the theory of quantum electrodynamics.)

مواضيع ذات صلة

انعطاف صغير عند النجوم

ما الحرارة في الاندماج النووي

التسخين بالحقن بذرات متعادلة

الاندماج النووي في المختبر

Broken symmetries

Antimatter

Nuclear forces

د. سميرة موسى علي، الإبداع في الفيزياء النووية

داخل النواة

أجهزة الإنذار الشخصية: عدادات الشارة

أجهزة الإنذار الشخصية: العدادات الجيبية

أجهزة الإنذار الشخصية Personnel Monitoring