Statistical Range
المؤلف:
Feller, W.
المصدر:
An Introduction to Probability Theory and Its Applications, Vol. 1, 3rd ed. New York: Wiley, 1968.
الجزء والصفحة:
...
10-2-2021
1613
Statistical Range
The term "range" has two completely different meanings in statistics.
Given order statistics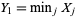 
, 
, ..., 
, 
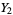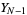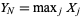, the range of the random sample is defined by
 |
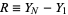(1)
|
(Hogg and Craig 1995, p. 152).
For small samples, the range is a good estimator of the population standard deviation (Kenney and Keeping 1962, pp. 213-214).
For a continuous uniform distribution
![P(x)=<span style=]() {1/C for 0<x<C; 0 for |x|>C, " src="https://mathworld.wolfram.com/images/equations/StatisticalRange/NumberedEquation2.gif" style="height:62px; width:160px" /> |
(2)
|
the distribution of the range is given by
 |
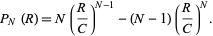(3)
|
This is illustrated above for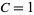 
and values of 
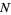from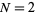 
(red) to 
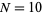(violet).
Given two samples with sizes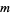 
and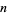 
and ranges 
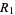and 
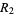, let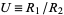 
. Then
![D(u)=<span style=]() {(m(m-1)n(n-1))/((m+n)(m+n-1)(m+n-2))[(m+n)u^(m-2)-(m+n-2)u^(m-1)]; for 0<=u<=1; (m(m-1)n(n-1))/((m+n)(m+n-1)(m+n-2))[(m+n)u^(-n)-(m+n-2)u^(-n-1)]; for 1<=u<infty. " src="https://mathworld.wolfram.com/images/equations/StatisticalRange/NumberedEquation4.gif" style="height:126px; width:418px" /> |
(4)
|
The mean is
 |
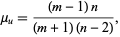(5)
|
and the mode is
![u^^=<span style=]() {((m-2)(m+n))/((m-1)(m+n-2)) for m-n<=2; ((n+1)(m+n-2))/(n(m+n)) for m-n>=2 " src="https://mathworld.wolfram.com/images/equations/StatisticalRange/NumberedEquation6.gif" style="height:84px; width:235px" /> |
(6)
|
(Kenney and Keeping 1962).
REFERENCES:
Feller, W. An Introduction to Probability Theory and Its Applications, Vol. 1, 3rd ed. New York: Wiley, 1968.
Hogg, R. V. and Craig, A. T. Introduction to Mathematical Statistics, 5th ed. New York: Macmillan, p. 152, 1995.
Kenney, J. F. and Keeping, E. S. "The Range." §6.2 in Mathematics of Statistics, Pt. 1, 3rd ed. Princeton, NJ: Van Nostrand, pp. 75-76, 213-214, 1962.
الاكثر قراءة في الاحتمالات و الاحصاء
اخر الاخبار
اخبار العتبة العباسية المقدسة
