The probability density function (PDF) 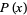 of a continuous distribution is defined as the derivative of the (cumulative) distribution function ,

			(1)
			(2)
			(3)

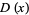so

			(4)
			(5)

A probability function satisfies

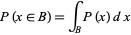(6)

and is constrained by the normalization condition,

			(7)
			(8)

Special cases are

			(9)
			(10)
			(11)
			(12)
			(13)

To find the probability function in a set of transformed variables, find the Jacobian. For example, If 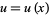, then

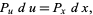(14)

so

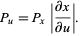(15)

Similarly, if 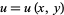 and 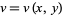, then

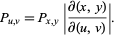(16)

Given 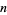 probability functions 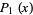, , 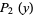..., 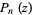, the sum distribution  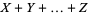has probability function

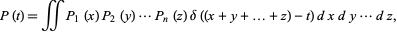(17)

where 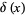 is a delta function. Similarly, the probability function for the distribution of  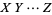is given by

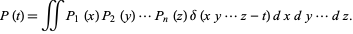(18)

The difference distribution 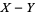 has probability function

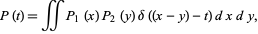(19)

and the ratio distribution 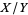 has probability function

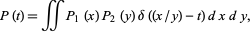(20)

Given the moments of a distribution (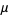, , 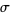and the gamma statistics 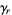), the asymptotic probability function is given by

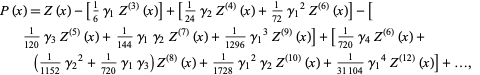(21)

where

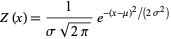(22)

is the normal distribution, and

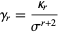(23)

for 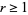 (with 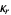 cumulants and  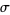the standard deviation; Abramowitz and Stegun 1972, p. 935).

REFERENCES:

Abramowitz, M. and Stegun, I. A. (Eds.). "Probability Functions." Ch. 26 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 925-964, 1972.

Evans, M.; Hastings, N.; and Peacock, B. "Probability Density Function and Probability Function." §2.4 in Statistical Distributions, 3rd ed. New York: Wiley, pp. 9-11, 2000.

McLaughlin, M. "Common Probability Distributions." http://www.geocities.com/~mikemclaughlin/math_stat/Dists/Compendium.html.

Papoulis, A. Probability, Random Variables, and Stochastic Processes, 2nd ed. New York: McGraw-Hill, p. 94, 1984.