

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Random Walk--1-Dimensional
المؤلف:
Abramowitz, M. and Stegun, I. A.
المصدر:
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover
الجزء والصفحة:
...
24-3-2021
4278
Random Walk--1-Dimensional
Let 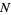 steps of equal length be taken along a line. Let
steps of equal length be taken along a line. Let 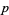 be the probability of taking a step to the right,
be the probability of taking a step to the right, 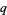 the probability of taking a step to the left,
the probability of taking a step to the left, 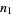 the number of steps taken to the right, and
the number of steps taken to the right, and 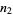 the number of steps taken to the left. The quantities
the number of steps taken to the left. The quantities 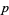 ,
, 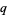 ,
, 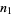 ,
, 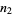 , and
, and 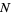 are related by
are related by
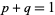 |
(1) |
and
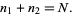 |
(2) |
Now examine the probability of taking exactly 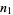 steps out of
steps out of 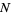 to the right. There are
to the right. There are 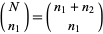 ways of taking
ways of taking 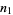 steps to the right and
steps to the right and 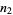 to the left, where
to the left, where 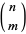 is a binomial coefficient. The probability of taking a particular ordered sequence of
is a binomial coefficient. The probability of taking a particular ordered sequence of 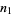 and
and 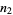 steps is
steps is 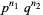 . Therefore,
. Therefore,
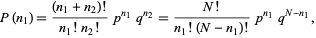 |
(3) |
where 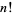 is a factorial. But this is simply a binomial distribution, so the mean number of steps
is a factorial. But this is simply a binomial distribution, so the mean number of steps 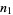 to the right is
to the right is
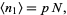 |
(4) |
and the mean number of steps to the left is
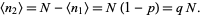 |
(5) |
Similarly, the variance is given by
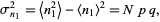 |
(6) |
and the root-mean-square deviation is
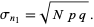 |
(7) |
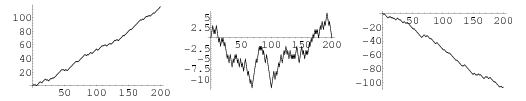
Consider now the distribution of the distances 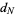 traveled after a given number of steps,
traveled after a given number of steps,
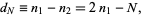 |
(8) |
as opposed to the number of steps in a given direction. The above plots show 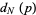 for
for  and three values
and three values 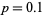 ,
, 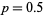 , and
, and 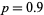 , respectively. Clearly, weighting the steps toward one direction or the other influences the overall trend, but there is still a great deal of random scatter, as emphasized by the plot below, which shows three random walks all with
, respectively. Clearly, weighting the steps toward one direction or the other influences the overall trend, but there is still a great deal of random scatter, as emphasized by the plot below, which shows three random walks all with 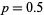 .
.

Surprisingly, the most probable number of sign changes in a walk is 0, followed by 1, then 2, etc.
For a random walk with 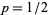 , the probability
, the probability 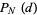 of traveling a given distance
of traveling a given distance 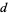 after
after 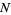 steps is given in the following table.
steps is given in the following table.
| steps | 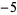 |
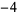 |
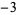 |
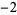 |
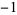 |
0 | 1 | 2 | 3 | 4 | 5 |
| 0 | 1 | ||||||||||
| 1 | 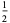 |
0 | 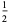 |
||||||||
| 2 | 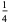 |
0 | 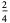 |
0 | 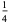 |
||||||
| 3 | 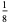 |
0 | 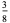 |
0 | 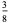 |
0 | 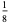 |
||||
| 4 | 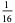 |
0 | 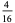 |
0 | 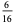 |
0 | 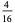 |
0 | 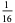 |
||
| 5 | 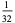 |
0 | 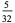 |
0 | 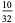 |
0 | 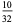 |
0 | 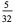 |
0 | 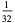 |
In this table, subsequent rows are found by adding half of each cell in a given row to each of the two cells diagonally below it. In fact, it is simply Pascal's triangle padded with intervening zeros and with each row multiplied by an additional factor of 1/2. The coefficients in this triangle are given by
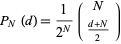 |
(9) |
(Papoulis 1984, p. 291). The moments
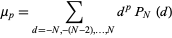 |
(10) |
of this distribution of signed distances are then given by
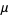 |
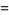 |
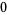 |
(11) |
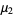 |
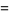 |
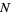 |
(12) |
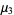 |
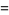 |
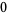 |
(13) |
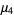 |
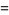 |
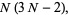 |
(14) |
so the mean is 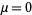 , the skewness is
, the skewness is 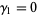 , and the kurtosis excess is
, and the kurtosis excess is
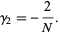 |
(15) |
The expectation value of the absolute distance after 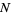 steps is therefore given by
steps is therefore given by
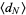 |
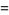 |
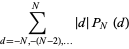 |
(16) |
 |
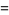 |
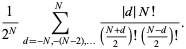 |
(17) |
This sum can be done symbolically by separately considering the cases 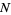 even and
even and 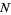 odd. First, consider even
odd. First, consider even 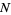 so that
so that 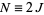 . Then
. Then
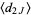 |
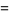 |
![(N!)/(2^N)[sum_(d=-2J,; -2(J-1),...)^(-2)(|d|)/(((2J+d)/2)!((2J-d)/2)!)+0+sum_(d=2,4,...)^(2J)(|d|)/(((2J+d)/2)!((2J-d)/2)!)]](https://mathworld.wolfram.com/images/equations/RandomWalk1-Dimensional/Inline85.gif) |
(18) |
 |
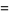 |
![(N!)/(2^N)[sum_(d=-J,-(J-1),...)^(-1)(|2d|)/(((2J+2d)/2)!((2J-2d)/2)!)+sum_(d=1,2,...)^(J)(|2d|)/(((2J+2d)/2)!((2J-2d)/2)!)]](https://mathworld.wolfram.com/images/equations/RandomWalk1-Dimensional/Inline88.gif) |
(19) |
 |
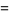 |
![(N!)/(2^N)[2sum_(d=1)^(J)(2d)/((J+d)!(J-d)!)]](https://mathworld.wolfram.com/images/equations/RandomWalk1-Dimensional/Inline91.gif) |
(20) |
 |
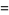 |
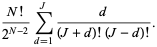 |
(21) |
But this sum can be evaluated analytically as
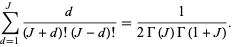 |
(22) |
Writing 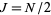 , plugging back in, and simplifying gives
, plugging back in, and simplifying gives
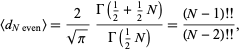 |
(23) |
where 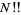 is the double factorial.
is the double factorial.
Now consider 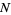 odd, so
odd, so 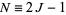 . Then
. Then
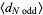 |
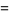 |
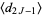 |
(24) |
 |
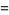 |
![(N!)/(2^N)[sum_(d=-(2J-1),; -(2J+1),...)^(-1)(|d|)/(((2J-1+d)/2)!((2J-1-d)/2)!)+sum_(d=1,3,...)^(2J-1)(|d|)/(((2J-1+d)/2)!((2J-1-d)/2)!)]](https://mathworld.wolfram.com/images/equations/RandomWalk1-Dimensional/Inline104.gif) |
(25) |
 |
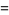 |
![(N!)/(2^(N-1))[sum_(d=1,3,...)^(2J-1)d/(((2J-1+d)/2)!((2J-1-d)/2)!)]](https://mathworld.wolfram.com/images/equations/RandomWalk1-Dimensional/Inline107.gif) |
(26) |
 |
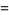 |
![(N!)/(2^(N-1))[sum_(d=2,4,...)^(2J)(d-1)/(((2J-2+d)/2)!((2J-d)/2)!)]](https://mathworld.wolfram.com/images/equations/RandomWalk1-Dimensional/Inline110.gif) |
(27) |
 |
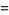 |
![(N!)/(2^(N-1))[sum_(d=1)^(J)(2d-1)/((J+d-1)!(J-d)!)].](https://mathworld.wolfram.com/images/equations/RandomWalk1-Dimensional/Inline113.gif) |
(28) |
But this sum can be evaluated analytically as
![sum_(d=1)^J(2d-1)/((J+d-1)!(J-d)!)=1/([Gamma(J)]^2).](https://mathworld.wolfram.com/images/equations/RandomWalk1-Dimensional/NumberedEquation14.gif) |
(29) |
Writing 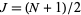 , plugging back in, and simplifying gives
, plugging back in, and simplifying gives
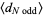 |
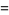 |
![(N!)/(2^(N-1)[Gamma(1/2+1/2N)]^2)](https://mathworld.wolfram.com/images/equations/RandomWalk1-Dimensional/Inline117.gif) |
(30) |
 |
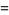 |
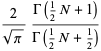 |
(31) |
 |
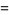 |
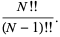 |
(32) |
Both the even and odd solutions can be written in terms of 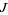 as
as
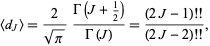 |
(33) |
or explicitly in terms of 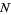 as
as
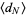 |
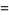 |
](https://mathworld.wolfram.com/images/equations/RandomWalk1-Dimensional/Inline128.gif) |
(34) |
 |
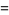 |
(35) |
The first few values of 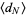 for
for 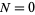 , 1, ... are therefore 0, 1, 1, 3/2, 3/2, 15/8, 15/8, 35/16, 35/16, ... (OEIS A086116 and A060818; Abramowitz and Stegun 1972, Prévost 1933, Hughes 1995), where the terms of each pair are given by the generating function
, 1, ... are therefore 0, 1, 1, 3/2, 3/2, 15/8, 15/8, 35/16, 35/16, ... (OEIS A086116 and A060818; Abramowitz and Stegun 1972, Prévost 1933, Hughes 1995), where the terms of each pair are given by the generating function
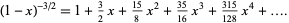 |
(36) |
These numbers also arise in the heads-minus-tails distribution.
Now, examine the asymptotic behavior of 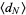 . The asymptotic expansion of the gamma function ratio is
. The asymptotic expansion of the gamma function ratio is
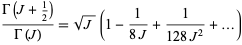 |
(37) |
(Graham et al. 1994), so plugging in the expression for 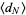 gives the asymptotic series
gives the asymptotic series
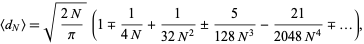 |
(38) |
where the top signs are taken for 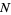 even and the bottom signs for
even and the bottom signs for 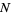 odd. Therefore, for large
odd. Therefore, for large 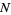 ,
,
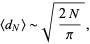 |
(39) |
which is also shown by Grünbaum (1960), Mosteller et al. (1961, p. 14), and König et al. (1999).
Tóth (2000) has proven that there are no more than three most-visited sites in a simple symmetric random walk in one dimension with unit steps.
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 798, 1972.
Chandrasekhar, S. "Stochastic Problems in Physics and Astronomy." Rev. Modern Phys. 15, 1-89, 1943. Reprinted in Selected Papers on Noise and Stochastic Processes (Ed. N. Wax). New York: Dover, pp. 3-91, 1954.
Erdős, P. and Révész, P. "On the Favourite Points of Random Walks." Math. Structures--Comput. Math.--Math. Model. (Sofia) 2, 152-157, 1984.
Erdős, P. and Révész, P. "Problems and Results on Random Walks." In Mathematical Statistics and Probability Theory, Vol. B: Statistical Inference and Methods. Proceedings of the Sixth Pannonian Symposium on Mathematical Statistics Held in Bad Tatzmannsdorf, September 14-20, 1986 (Ed. P. Bauer, F. Koneczny, and W. Wertz). Dordrecht, Netherlands: Reidel, pp. 59-65, 1987.
Feller, W. Ch. 3 in An Introduction to Probability Theory and Its Applications, Vol. 1, 3rd ed., rev. printing. New York: Wiley, 1968.
Gardner, M. "Random Walks and Gambling." Ch. 6 in Mathematical Circus: More Puzzles, Games, Paradoxes, and Other Mathematical Entertainments. Washington, DC: Math. Assoc. Amer., pp. 66-74, 1992.
Graham, R. L.; Knuth, D. E.; and Patashnik, O. Answer to problem 9.60 in Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, 1994.
Grünbaum, B. "Projection Constants." Trans. Amer. Math. Soc. 95, 451-465, 1960.
Hersh, R. and Griego, R. J. "Brownian Motion and Potential Theory." Sci. Amer. 220, 67-74, 1969.
Hughes, B. D. Eq. (7.282) in Random Walks and Random Environments, Vol. 1: Random Walks. New York: Oxford University Press, p. 513, 1995.
Kac, M. "Random Walk and the Theory of Brownian Motion." Amer. Math. Monthly 54, 369-391, 1947. Reprinted in Selected Papers on Noise and Stochastic Processes (Ed. N. Wax). New York: Dover, pp. 295-317, 1954.
König, H.; Schütt, C.; and Tomczak-Jaegermann, N. "Projection Constants of Symmetric Spaces and Variants of Khintchine's Inequality." J. reine angew. Math. 511, 1-42, 1999.
Mosteller, F.; Rourke, R. E. K.; and Thomas, G. B. Probability and Statistics. Reading, MA: Addison-Wesley, 1961.
Papoulis, A. "Random Walk." Probability, Random Variables, and Stochastic Processes, 2nd ed. New York: McGraw-Hill, pp. 290-291, 1984.
Prévost, G. Tables de Fonctions Sphériques. Paris: Gauthier-Villars, pp. 156-157, 1933.
Révész, P. Random Walk in Random and Non-Random Environment. Singapore: World Scientific, 1990.
Sloane, N. J. A. Sequences A060818 and A086116 in "The On-Line Encyclopedia of Integer Sequences."
Tóth, B. "No More than Three Favourite Sites for Simple Random Walk." 26 Apr 2000. https://arxiv.org/abs/math.PR/0004164.
Tóth, B. and Werner, W. "Tied Favourite Edges for Simple Random Walk." Combin., Prob., Comput. 6, 359-369, 1997.
Trott, M. "The Mathematica Guidebooks Additional Material: Random Walk with Varying Step Size." https://www.mathematicaguidebooks.org/additions.shtml#N_1_01.
 الاكثر قراءة في الاحتمالات و الاحصاء
الاكثر قراءة في الاحتمالات و الاحصاء
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















