Least Squares Fitting--Polynomial
المؤلف:
المرجع الالكتروني للمعلوماتيه
المصدر:
www.almerja.com
الجزء والصفحة:
...
29-3-2021
1901
Least Squares Fitting--Polynomial
Generalizing from a straight line (i.e., first degree polynomial) to a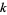 
th degree polynomial
 |
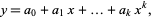(1)
|
the residual is given by
![R^2=sum_(i=1)^n[y_i-(a_0+a_1x_i+...+a_kx_i^k)]^2.](https://mathworld.wolfram.com/images/equations/LeastSquaresFittingPolynomial/NumberedEquation2.gif) |
(2)
|
The partial derivatives (again dropping superscripts) are
These lead to the equations
or, in matrix form
![[n sum_(i=1)^(n)x_i ... sum_(i=1)^(n)x_i^k; sum_(i=1)^(n)x_i sum_(i=1)^(n)x_i^2 ... sum_(i=1)^(n)x_i^(k+1); | | ... |; sum_(i=1)^(n)x_i^k sum_(i=1)^(n)x_i^(k+1) ... sum_(i=1)^(n)x_i^(2k)][a_0; a_1; |; a_k]=[sum_(i=1)^(n)y_i; sum_(i=1)^(n)x_iy_i; |; sum_(i=1)^(n)x_i^ky_i].](https://mathworld.wolfram.com/images/equations/LeastSquaresFittingPolynomial/NumberedEquation3.gif) |
(9)
|
This is a Vandermonde matrix. We can also obtain the matrix for a least squares fit by writing
![[1 x_1 ... x_1^k; 1 x_2 ... x_2^k; | | ... |; 1 x_n ... x_n^k][a_0; a_1; |; a_k]=[y_1; y_2; |; y_n].](https://mathworld.wolfram.com/images/equations/LeastSquaresFittingPolynomial/NumberedEquation4.gif) |
(10)
|
Premultiplying both sides by the transpose of the first matrix then gives
![[1 1 ... 1; x_1 x_2 ... x_n; | | ... |; x_1^k x_2^k ... x_n^k][1 x_1 ... x_1^k; 1 x_2 ... x_2^k; | | ... |; 1 x_n ... x_n^k][a_0; a_1; |; a_k]
=[1 1 ... 1; x_1 x_2 ... x_n; | | ... |; x_1^k x_2^k ... x_n^k][y_1; y_2; |; y_n],](https://mathworld.wolfram.com/images/equations/LeastSquaresFittingPolynomial/NumberedEquation5.gif) |
(11)
|
so
![[n sum_(i=1)^(n)x_i ... sum_(i=1)^(n)x_i^k; sum_(i=1)^(n)x_i sum_(i=1)^(n)x_i^2 ... sum_(i=1)^(n)x_i^(k+1); | | ... |; sum_(i=1)^(n)x_i^k sum_(i=1)^(n)x_i^(k+1) ... sum_(i=1)^(n)x_i^(2k)][a_0; a_1; |; a_k]=[sum_(i=1)^(n)y_i; sum_(i=1)^(n)x_iy_i; |; sum_(i=1)^(n)x_i^ky_i].](https://mathworld.wolfram.com/images/equations/LeastSquaresFittingPolynomial/NumberedEquation6.gif) |
(12)
|
As before, given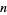 
points 
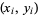and fitting with polynomial coefficients 
, ..., 
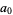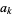gives
![[y_1; y_2; |; y_n]=[1 x_1 x_1^2 ... x_1^k; 1 x_2 x_2^2 ... x_2^k; | | | ... |; 1 x_n x_n^2 ... x_n^k][a_0; a_1; |; a_k],](https://mathworld.wolfram.com/images/equations/LeastSquaresFittingPolynomial/NumberedEquation7.gif) |
(13)
|
In matrix notation, the equation for a polynomial fit is given by
 |
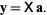(14)
|
This can be solved by premultiplying by the transpose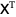 
,
 |
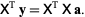(15)
|
This matrix equation can be solved numerically, or can be inverted directly if it is well formed, to yield the solution vector
 |
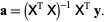(16)
|
Setting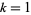 
in the above equations reproduces the linear solution.
الاكثر قراءة في الاحتمالات و الاحصاء
اخر الاخبار
اخبار العتبة العباسية المقدسة
