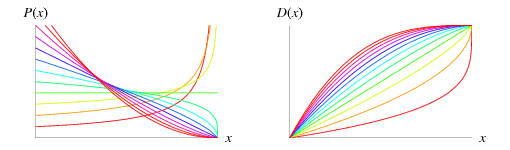
A general type of statistical distribution which is related to the gamma distribution. Beta distributions have two free parameters, which are labeled according to one of two notational conventions. The usual definition calls these 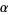 and 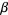, and the other uses  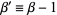and 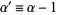 (Beyer 1987, p. 534). The beta distribution is used as a prior distribution for binomial proportions in Bayesian analysis (Evans et al. 2000, p. 34). 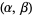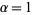The above plots are for various values of  with  and 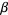 ranging from 0.25 to 3.00.

The domain is , and the probability function 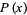 and distribution function  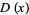are given by

			(1)
			(2)
			(3)

where 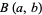 is the beta function,  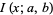is the regularized beta function, and 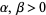. The beta distribution is implemented in the Wolfram Language as BetaDistribution[alpha, beta].

The distribution is normalized since

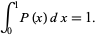(4)

The characteristic function is

			(5)
			(6)

where 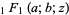 is a confluent hypergeometric function of the first kind.

The raw moments are given by

			(7)
			(8)

(Papoulis 1984, p. 147), and the central moments by

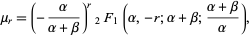(9)

where 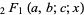 is a hypergeometric function.

The mean, variance, skewness, and kurtosis excess are therefore given by

			(10)
			(11)
			(12)
			(13)

The mode of a variate distributed a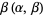s  is

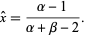(14)

REFERENCES:

Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 944-945, 1972.

Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 534-535, 1987.

Evans, M.; Hastings, N.; and Peacock, B. "Beta Distribution." Ch. 5 in Statistical Distributions, 3rd ed. New York: Wiley, pp. 34-42, 2000.

Jambunathan, M. V. "Some Properties of Beta and Gamma Distributions." Ann. Math. Stat. 25, 401-405, 1954.

Kolarski, I. "On Groups of 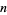 Independent Random Variables whose Product Follows the Beta Distribution." Colloq. Math. IX Fasc. 2, 325-332, 1962.

Krysicki, W. "On Some New Properties of the Beta Distribution." Stat. Prob. Let. 42, 131-137, 1999.

Papoulis, A. The Fourier Integral and Its Applications. New York: McGraw-Hill, 1962.