خصائص النيوترون

1- دلت تجارب التشتت وتجارب أخرى في الميادين المختلفة على أن كتلة النيوترون هي أكبر من كتلة البروتون وأنها تساوي 1.008665 و.ك.ذ وهذه تعادل: 939.55 م.ا.ف.

2- يمكن للنيوترون (الحر) أن يتحلل حب العلاقة التالية:

(1)..........

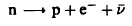
حيث ينتج البروتون وتنطلق جسيمات ^-β وضديدات النيوترينو 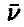. وقد دلت التجارب على أن عمر النصف Half-life للنيوترون يقدر بحوالي 12 دقيقة.

وهناك تقنية معروفة لتقدير عمر النصف للنيوترون وذلك بتوجيه شعاع نيوتروني ينطلق من مفاعل نووي نحو حيز مفرغ من الهواء حيث تتحلل بعض الجسيمات ومن ثم يمكن الكشف عن نواتج التفاعل (جسيمات β) ومن ثم تقدير عمر النصف للنيوترون.

3- تصنف النيوترونات حسب طاقتها إلى مجموعة من الأقسام. وبالرغم من أنه لا توجد حدود واضحة بين هذه الأقسام إلا أن هذا التقيم يتيح لنا تصنيف النيوترونات حسب الجدول رقم (1). عندما تخترق النيوترونات مادة ما فإنها تأخذ في التصادم مع أنوية المادة حيث ينتج عن ذلك فقد في الطاقة. وباستمرار التصادم يستمر الفقد في الطاقة. حتى تصل هذه النيوترونات إلى اتزان حراري  Thermal Equilibrium مع جزيئات المادة تماماً كما تفعل ذلك جزيثات الغاز. فإذا كانت درجة حرارة المادة هي درجة حرارة الغرفة فإن هذه النيوترونات تعرف بالنيوترونات الحرارية Thermal Neutrons وسوف تتبع طاقة هذه النيوترونات توزيع ماكسويل حول القيمة المتوسطة وتعطي بالعلاقة:

(2) .............

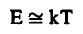
حيث هي ثابت بولتزمان (K = 8.61 × 10^-11 Mev/K).

τ درجة الحرارة (مقدرة بالكلفن)

وبالتالي يمكن تقدير طاقة النيوترون الحراري إذا فرضنا أن درجة حرارة الغرقة هي C 27 وينتج أن E = 0.025 ev.

كما ويمكن حساب سرعة النيوترونات الحرارية باستخدام العلاقة:

(4.11)       ........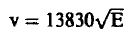

حيث E تقدر بوحدات أف.

وتنتج v بوحدات م/ت (m/s).

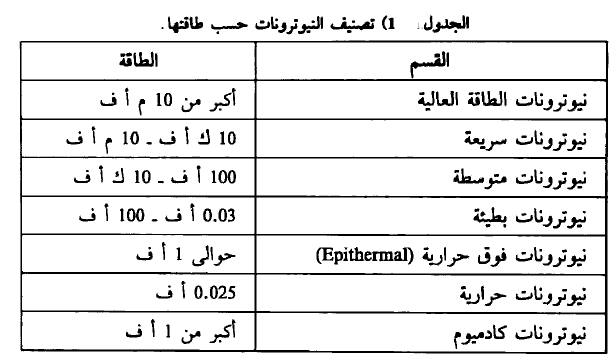
يطلق على النيوترونات التي تزداد طاقتها عن 1 أ. ف. أحياناً نيوترونات الكادميوم وذلك لأن الكادميوم يتميز بمعدل امتصاص عال للنيوترونات ذات الطاقات الأقل من حوالي 0.4 أ.ف. بينما يتخفض هذا المعدل كثيراً عندما تغوق طاقات النيوترونات 1 أ.ف. ومن ثم يعتبر الكادميوم «منفذا» للنيوترونات الأخيرة. ولذلك تعرف على هذه النيوترونات بنيوترونات الكادميوم.

ويمكن قياس طاقة النيوترون بعدة تقنيات مختلفة حسب هذه الطاقة. فعندما تكون في حدود م.أ.ف. فإننا نستخدم تقنية زمن الطيران   Time -of-Flight حيث يترك النيوترون ليطير - ينتقل - بين نقطتين تفصلهما مسافة معينة وبتعين زمن الطيران يمكن تقدير سرعة ومن ثم طاقة هذا النيوترون أما عندما تقع طاقة النيوترون في حدود أ.ف فإننا نستخدم تقنية حيود Diffraction النيوترون وقانون براغ.

مواضيع ذات صلة

انعطاف صغير عند النجوم

ما الحرارة في الاندماج النووي

التسخين بالحقن بذرات متعادلة

الاندماج النووي في المختبر

Broken symmetries

Antimatter

Nuclear forces

د. سميرة موسى علي، الإبداع في الفيزياء النووية

داخل النواة

أجهزة الإنذار الشخصية: عدادات الشارة

أجهزة الإنذار الشخصية: العدادات الجيبية

أجهزة الإنذار الشخصية Personnel Monitoring