أخطاء القياس

يعتبر تقييم الخطأ عند القيام بتجربة ما ذا أهمية كبيرة إذ يحدد صحة ودقة التجربة. وتتنوع مصادر الأخطاء العملية. فهناك أخطاء ناتجة عن دقة الشخص الذي يقوم بإجراء التجربة وأخطاء اخرى ناتجة عن دقة الأجهزة نفسها ومدى استقرار أدائها. كما توجد هناك أخطاء ناتجة عن طبيعة الكمية الطبيعية المراد قياسها. ففي حالة قياس النشاط الإشعاعي لمادة ما مثلاً فإننا نجد أن هذا التفاعل يتم عشوائياً. ويعتمد عدد الانحلالات في وحدة الزمن على عدد الأنوية الموجودة عند لحظة زمنية وعلى ثابت الانحلال ومن ثملا د من معالجة التفاوتات الإحصائية في معدل العد بقوانين الاحتمالات فإذا قمنا بتسجيل معدل العد عدة مرات فإننا في كل مرة سنحصل على قيمة مختلفة عن سابقتها. فمن من هذه القراءات هو عبارة عن القراءة الحقيقية؟ إن صعوبة الإجابة عن هذا السؤال تجعلنا نطرح فكرة إدخال مفهوم متوسط القراءات المقاسة.

1- القيمة المتوسطة The Mean Value

لنفترض أننا نقوم بتسجيل المعدودات الناتجة عن مادة مشعة باستخدام عداد جايجر وأننا نقوم بتسجيل المعدودات لفترات زمنية متساوية (t) ثانية. ولنفترض أننا كررنا هذه القرارات (n) من المرات. ولنفترض أن إحدى هذه القراءات هي X_i وبالتالي تنتج لدينا البيانات:

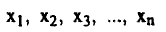
فتكون القيمة المتوسطة لهذه القراءات هي:

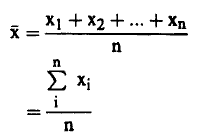................(1)

2- الانحراف عن القيمة المتوسطة (α)

يمكن تعريف الانحراف عن القيمة المتوسطة (α) بالعلاقة:

(1)..............

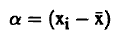
أي أنه عبارة عن انحراف أي قراءة ولتكن (_ix) عن القيمة المتوسطة .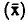

لاحظ أن مجموع الانحرافات عن القيمة المتوسطة يساوي صفراً. أي أن:

(2)..........

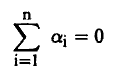
3- الانحراف المعياري (σ) Standard Deviation

يمكن تعريف الانحراف المعياري بالعلاقة:

(3).............

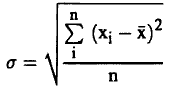
ويعرف مربع هذه الكمية (σ²) بالمقياس أو The Variance أي أن:

(4)...........

4- نماذج إحصائية

أ) توزيع ذات الحدين Binomial Distribution

إذا كان لدينا (N) نواة تتحلل بثابت قدره (λ) فإن احتمال (P(n رصد (n) انحلاله في زمن (t) يعطي بالعلاقة التي تعرف بتوزيع ذي الحدين:

(5)................

يمكن تبسيط هذه العلاقة في حالة المواد المشعة حيث نجد أنه عندما يكون 1 >> λt أي أن فترة القياس أصغر كثيراً من عمر النصف للمادة وبافتراض أن عدد الأنوية الذرية كبير جداً 1<<N وأن n<< N. ومن ثم يمكن استنتاج توزيعاً جديداً هو توزيع بواسن.

ب) توزيع بواسون Poisson Distribution

ويعطي الاحتمال (P(n هنا بالعلاقة:

(6)...........

حيث 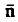هي متوسط الانحلالات.

ج- توزيع جاوس Gaussian Distribution

إذا كان عدد القراءات (n) كبيراً بما فيه الكفاية (100 < < n) فإننا نحصل على توزيع جاوس أي أن:

(7).............

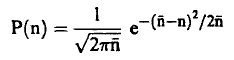
لقد وجد أن توزيع جاوس وتوزيع بواسون متقاربين حتى عندما تهبط 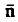إلى 15 معدوده/ دقيقة أو أقل. ويبين الشكل (1) هاذين التوزيعين عندما 15 = .

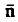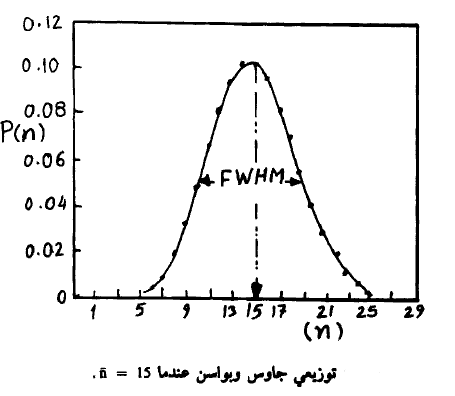
الشكل (1)

مواضيع ذات صلة

انعطاف صغير عند النجوم

ما الحرارة في الاندماج النووي

التسخين بالحقن بذرات متعادلة

الاندماج النووي في المختبر

Broken symmetries

Antimatter

Nuclear forces

د. سميرة موسى علي، الإبداع في الفيزياء النووية

داخل النواة

أجهزة الإنذار الشخصية: عدادات الشارة

أجهزة الإنذار الشخصية: العدادات الجيبية

أجهزة الإنذار الشخصية Personnel Monitoring