معامل التضاعف Multiplication Factor

يمكن الآن تعريف هذا المعامل على أنه النسبة بين عدد النيوترونات الناتجة (والتي سوف تمتص) في جيل معين وعدد النيوترونات الناتجة (أو الممتصة) في الجيل السابق له. أي أن:

(1)...........

وبصورة خاصة إذا كانت المنظومة لدينا لانهائية فإننا نعرف معامل التضاعف اللانهائي _∞​K حيث:

(2)............

وتعرف هذه المعادلة المهمة بصيغة المعاملات الأربعة. حيث يمكن تعيين _∞​K بمعرفة الأربعة عوامل ∋ ,f, P, η. وقد بينا كيف يمكن حساب كل منها. معامل التضاعف اللانهائي (_∞​K) صحيح إذا كانت لدينا منظومة لانهائية، اما تحت الظروف العادية فإنه توجد لدينا منظومة ذات حجم وحيز محدد. وهذا هو الحال عندما نقوم ببناء مفاعل ما. إذ أنه سيكون ذا أبعاد واضحة ومحددة. في هذه الحالة نجد انه علينا تعديل بعض شروطنا السابقة، إذ نجد هنا أن بعض النيوترونات سيتمكن من الهرب Escape من المنظومة ومن ثم لن تمتص جميع النيوترونات داخل المنظومة. ومن ثم علينا تعريف معامل تضاعف فعلي K_eff) Effective Multiplication Factor) حيث:

مما سبق يتضح لنا أنه في حالة المنظومة المحدودة فإن بعضاً من النيوترونات سوف يتمكن من الهرب خارج المنظومة. وبالتالي يمكننا إدخال مفهوم احتمال عدم التسرب (nonleakage Propability (P الذي يعبر عن احتمال عدم تسرب النيوترونات خارج المنظومة المحدودة. وإنما تظل هذه النيوترونات داخل المنظومة إلى أن تمتص جميعها. وبالتالي نجد أن:

أي أن:

(3).........

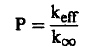
وبالتالي فإن:

(4)..........

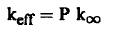
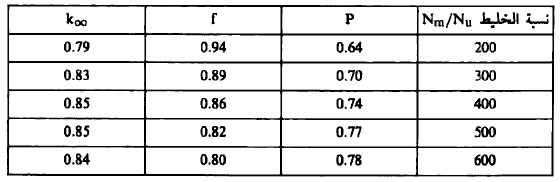
نبين في الجدول (1) بعض المعاملات الخاصة بخليط متجانس من اليورانيوم الطبيعي والجرافيت.

الجدول (1) بعض المعاملات الخاصة بخليط متجانس من اليورانيوم الطبيعي والجرافيت (N_m عدد أنوية المهدئ (الجرافيت)، N_u عدد أنوية اليورانيوم).

مواضيع ذات صلة

انعطاف صغير عند النجوم

ما الحرارة في الاندماج النووي

التسخين بالحقن بذرات متعادلة

الاندماج النووي في المختبر

Broken symmetries

Antimatter

Nuclear forces

د. سميرة موسى علي، الإبداع في الفيزياء النووية

داخل النواة

أجهزة الإنذار الشخصية: عدادات الشارة

أجهزة الإنذار الشخصية: العدادات الجيبية

أجهزة الإنذار الشخصية Personnel Monitoring