زمن الانفجار

لكي يحدث انفجار لا بد أن يتم انشطار كتلة اليورانيوم (حوالي kg2) في زمن قصير جداً وليكن في حدود ميكروثانية (م). ولكي نفهم ذلك نعود إلى الانشطار النووي. فإذا بدأنا بعدد من النيوترونات (N₀) السريعة فإنه بعد مرور زمن قدره (t) يصبح العدد (N) حيث:

(1)................

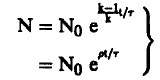
حيث ρ المفاعية.

K معامل الإنتاج.

τ الزمن المتوسط بين انشطارين متتاليين (في حدود⁹ S ^-10).

t فترة زمنية معينة، وليكن الزمن اللازم لحدوث الانفجار وتساوي ⁶s^-10 .

فإذا كانت K أكبر قليلاً من 1 ولتكن 1.1 فإن:

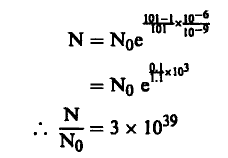
هذا يعني أن عدد النيوترونات بعد مرور ميكروثانية (s10^-6) سيتضاعف إلى 10³⁹ ضعفاً. فإذا كان لدينا Kg 2 من اليورانيوم فإنها تحتوي على  نواة. ومن ثم فإن عدد هذه النيوترونات سيكون كافياً لإحداث انشطار نووي لكل اليورانيوم، ومن ثم تتحرر الطاقة الناتجة عن هذا الانشطار في فترة زمنية تساوي ميكروثانية، وهذا هو الانفجار النوري.

مقارنة بين زمن الانفجار وزمن السيطرة على المفاعل:

أ- في حالة المفاعل:

سوف نأخذ في الاعتبار هنا النيوترونات الحرارية حيث يهبط هنا متوسط عمر النيرترون الناتج عن الانشطار في مفاعل الكربون إلى حوالي ميللي ثانية، وعند أخذ النيوترونات المتأخرة في الاعتبار نجد أن متوسط (τ) يهبط إلى حوالي s 0.1 ومن ثم إذا اعتبرنا أن 1.1 = K أو 0.1 = ρ فإن:

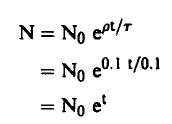
فإذا اعتبرنا 1μs = t فإن:

أي أن معدل نمو النيوترونات في المفاعل صغير جداً.

لنفترض الآن أنه لسبب ما أصبح لدينا:

فكيف يمكننا السيطرة على المفاعل؟

بتطبيق المعادلة السابقة نجد أن:

ومنها فإن:

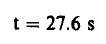
أي أن عدد النيوترونات قد تضاعف إلى 1012 في زمن قدره 28 ثانية تقريباً وهذه فترة زمنية كافية للسيطرة على المفاعل وذلك بتحريك قضبان التحكم لامتصاص العدد الزائد من النيوترونات. من الجدير بالذكر هنا أن نذكر أنه في حالة المفاعل يلزمنا معرفة تاريخ حياة النيوترون منذ لحظة ولادته (عند الانشطار) وحتى يسبب (انشطاراً آخر لنواة أخرى وهذه الفترة معقدة جداً. ولكن تشغيل المفاعل يحتاج إلى المعرفة الدقيقة لهذه الفترة) .

ب-  في حالة القنبلة:

بتطبيق نفس المعادلة نجد أن :

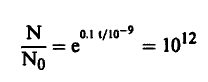
حيث عوضنا عن (τ) بزمن الانشطار (10^-9 s) ومنها نجد أن:

وبأخذ لوغاريتي الطرفين نجد أن:

وهذه فترة زمنية لا نستطيع أن نفعل شيئاً للسيطرة على النيوترونات أثنائها ومن ثم يحدث الانفجار النووي.

مواضيع ذات صلة

انعطاف صغير عند النجوم

ما الحرارة في الاندماج النووي

التسخين بالحقن بذرات متعادلة

الاندماج النووي في المختبر

Broken symmetries

Antimatter

Nuclear forces

د. سميرة موسى علي، الإبداع في الفيزياء النووية

داخل النواة

أجهزة الإنذار الشخصية: عدادات الشارة

أجهزة الإنذار الشخصية: العدادات الجيبية

أجهزة الإنذار الشخصية Personnel Monitoring