الزخم النظيري Isotopic Spin

يرمز للزخم النظيري بالرمز (I) وهو هنا لا علاقة له بالزخم الزاوي (J) أو الزخم المغزلي (S) ولكنه أدخل أصلاً من أجل التفريق بين البروتون والنيوترون لأن كليهما نيوكليون ولكن البروتون موجب الشحنة أما النيوترون فمتعادل الشحنة ٠ ومن ثم أدخل مفهوم الزخم النظيري ليدل على عدد حالات الشحنة التي يمكن أن توجد فيها مجموعة من الجسيمات المتشابهة. فإذا كان لمجموعة ما زخماً نظيرياً قدره (I) فإن عدد التضاعف (M) (عدد الجسيمات المختلفة الشحنة) يعطي بالعلاقة:

(1) ............

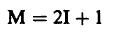
وذلك كما في حالة الزخم (ℓ) أو (S), (حيث (1 + 2ℓ= M)).

كما وتعرف أيضاً الرمز (I_z) على أنه يعبر عن مركبة I في اتجاه معين وليكن (Z) (في اتجاه فضاء الشحنة (Charge space)) . وذلك كما في (m) في حالة الزخم (ℓ). فمثلاً في حالة النيوكليونات فإننا سنعطيها الرقم 1/2= I وهذا يعني أن عدد حالات الجسيمات المشحونة (M) يساوي 1 + 1/2 × 2 ويساوي 2 أي أن هناك جسيمين. بشحنتين مختلفتين. وفي هذه الحالة. فإن: I_z = 1/2 (عدد المركبات) بحيث يعطي البروتون الموجب الشحنة I_z = +1/2 بينما يعطي للنيوترون (المتعادل الشحنة) الرقم: I_z = -1/2 وهكذا بالنسبة لباقي الجسيمات.

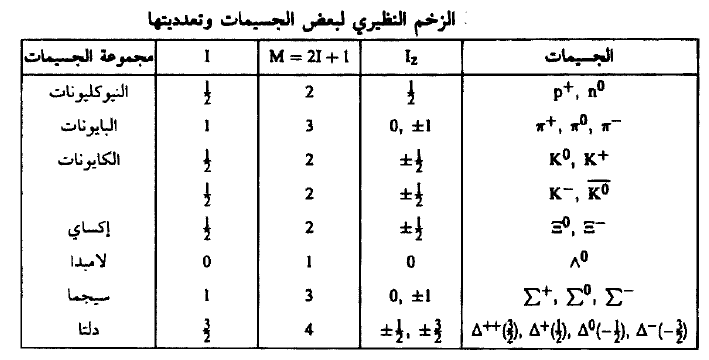
نبين في الجدول (1) الزخم النظيري لبعض الجسيمات وتعدديتها. وفي واقع الأمر يعبر (I) عن أن القوة النووية لا تعتمد على الشحنة الكهربية.

الجدول (1)

مواضيع ذات صلة

انعطاف صغير عند النجوم

ما الحرارة في الاندماج النووي

التسخين بالحقن بذرات متعادلة

الاندماج النووي في المختبر

Broken symmetries

Antimatter

Nuclear forces

د. سميرة موسى علي، الإبداع في الفيزياء النووية

داخل النواة

أجهزة الإنذار الشخصية: عدادات الشارة

أجهزة الإنذار الشخصية: العدادات الجيبية

أجهزة الإنذار الشخصية Personnel Monitoring