يتضمن هذا البند إعطاء صيغة نظامية لحل أنظمة المعادلات الخطية والتي تعتمد على فكرة اختزال المصفوفة الممتدة إلى شكل بسيط نستطيع من خلاله معرفة حل المعادلات الخطية بمجرد النظر إليها.

مثال (1): حل النظام الخطي الآتي:

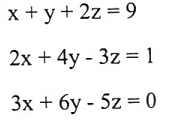
الحل:

1. نوجد المصفوفة الممتدة للنظام الخطي:

2. باستخدام سلسلة من عمليات الصف البسيط نستطيع الحصول على الصيغة المختزنة الآتية:

وتسمى هذه الصيغة، الصيغة المدرجة الصفية المختزلة، ولكي تكون المصفوفة بهذه الصيغة يجب أن تحقق الخواص الآتية:

a. إذ كانت عناصر صف ما ليست جميعها أصفاراً، فإن أول عدد غير صفري في الصف يجب أن يكون 1 ويسمى الدليل.

b. إذا وجد صف أما أو عدة صفوف جميع عناصرها أصفار فإنها توضع أسفل المصفوفة.

c. في أي صفين متعاقبين ليست جميع عناصرها أصفار، فإن الدليل 1 للصف الأسفل يكون أبعد إلى اليمين من الدليل 1 في الصف الأعلى.

d. كل عمري يحوي الدليل 1 تكون عناصره الاخرى صفر.

ملاحظة:

المصفوفة التي تحقق الشروط c, b, a فقط تسمى بالصيغة المدرجة الصفية.

مثال(1):

المصفوفات الآتي هي بالصيغة المدرجة الصفية المختزلة

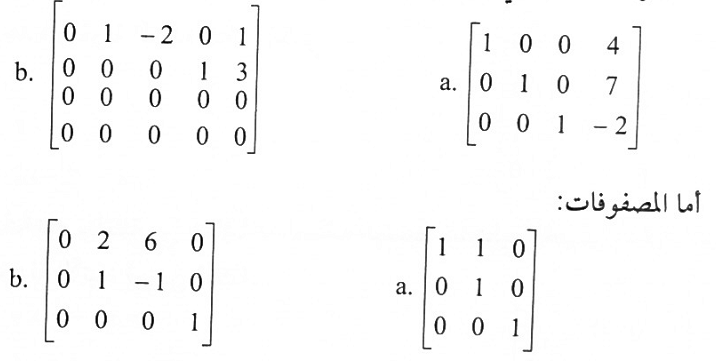
فهي بالصيغة المدرجة الصفية وليست بالصيغة المدرجة الصفية المختزلة.

مثال(2):

نفرض أن المصفوفات الآتية هي بالصيغة المدرجة الصفية المختزنة المكافئة لمصفوفات ممتدة. اوجد نظام المعادلات الخطية المقابلة لكل منهما.

الحل:

نظام المعادلات الخطية المقابلة للصيغة في a هو:

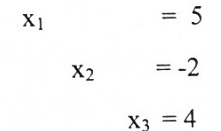
وبمجرد النظر لهذه النظام، نحصل على الحل x₁ = 5 , x₃ = 4 , x₂ = -2 أما النظام المقابل للصيغة في b فهو:

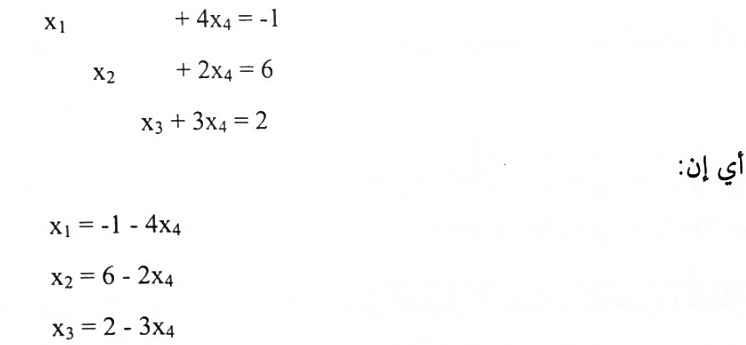
وبفرض x₄ = t (x₄ يسمى المتغير الحر و t  يسمى المتغير الوسيط).

فإن:

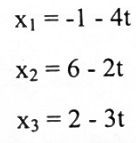
لاحظ أن هنالك عدد غير محدود من الحلول.

مثال (3):

اختزل المصفوفة الممتدة الآتية للصيغة المدرجة الصفية المختزلة.

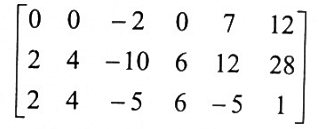
الحل:

1. لكي نجعل العنصر الأول في العمود الأول لا يساوي صفر نبادل الصف الأول بأي صف آخر. فمثلاً نبادل الصف الأول مع الصف الثاني وسنحصل على:

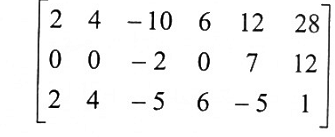
2. نجعل العدد الأول في الصف الأول يساوي 1 وذلك بضرب الصف الأول في 1/2 فنحصل على:

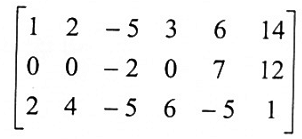
3. نجعل الأعداد في العمود الأول أسفل الدليل 1 مساوية للصفر، وذلك بضرب الصف الأول في -2 وإضافته للصف الثالث فنحصل على:

4. لكي نحصل على الدليل 1 في العمود الثالث نحول العدد -2 في الصف الثاني إلى 1 بضرب الصف الثاني في 1/2 فنحصل على:

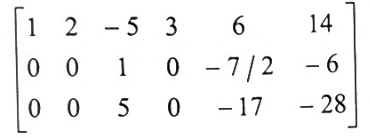
5. لكي نحصل على صفر أسفل الدليل 1 في الصف الثاني. نحول العدد 5 في الصف الثالث إلى صفر من خلال ضرب الصف الثاني في -5 وإضافته إلى الصف الثالث لنحصل على:

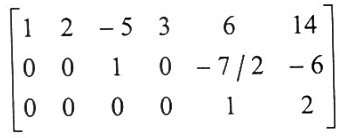
6. نحول العدد 1/2 في الصف الثالث للدليل 1 وذلك بضرب الصف الثالث في 2 فنحصل على:

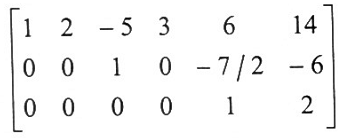
7. الصيغة الواردة في الفقرة (6) أعلاه هي الصيغة المدرجة الصفية ، ولكي نحصل على الصيغة المدرجة الصفية المختزلة نستمر بتطبيق عمليات الصف البسيطة.

8. نضرب الصف الثالث في 7/2 ونضيفه للصف الثاني فنحصل على:

9. نضرب الصف الثالث في -6 ونضيفه إلى الصف الاول لنحصل على

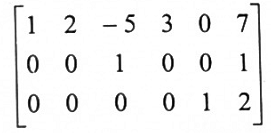
10. وأخيراً نضرب الصف الثاني في 5 ونضيفه للصف الأول فنحصل على:              

وهذا الشكل هو بالصيغة المدرجة الصفية المختزلة.

ملاحظة:

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم الشؤون الدينية يواصل إقامة محاضراته الفقهية في صحن مرقد أبي الفضل العباس (عليه السلام)

أكاديمية التطوير الإداري تنظم دورة في أمن المعلومات واستخدام تطبيقات الذكاء الاصطناعي

بذكرى وفاتها.. قسم الشؤون الفكريّة يستعرض إصدارًا عن خطاب السيدة زينب (عليها السلام) وتأثيره

قسم الشؤون الدينية يقيم دورة تطويرية لمنتسبي قسمي الحزام الأخضر الشمالي والجنوبي

المزيد

الآخبار الصحية

طبيب يكشف أفضل مكمل غذائي لتحسين المزاج ودعم الصحة النفسية

دراسة جديدة تكشف أضرار الأطعمة الجاهزة على القلب ؟

6 أطعمة طبيعية تهدئ الزكام دون أدوية.. تعرف عليهم

ماذا يحدث لأعراض الزكام عند تناول الثوم بانتظام؟

المزيد

الآخبار التكنلوجية

ابتكار ثوري في بطاريات السيارات الكهربائية.. سعة أعلى 4 مرات

ماذا يحدث لجسمك عند شرب الماء الساخن يوميا؟

7 فوائد "خفية" لشرب شاي الكركديه كل يوم

دراسة تكشف قدرة الحيتان على سماع الأصوات منخفضة وعالية التردد من مسافة بعيدة

المزيد

مواضيع ذات صلة

فضاء المتجهات الإقليدي-تمارين محلولة

فضاء المتجهات الإقليدي-تمارين محلولة

فضاء المتجهات الإقليدي-الفضاء الاقليدي النوني

فضاء المتجهات العام- فضاء المتجهات الحقيقي

فضاء المتجهات العام-رتبة المصفوفات بعد الفضاء الصفري

فضاء المتجهات العام-فضاء الصفوف وفضاء الأعمدة والفضاء الصفري

فضاء المتجهات العام- الأساس والبعد

فضاء المتجهات العام-الفضاءات الجزئية

فضاء الضرب الداخلي-الأساسات المتعامدة طريقة كرام ــ شمت

فضاء الضرب الداخلي-الضرب الداخلي

فضاء الضرب الداخلي-المصفوفات المتعامدة، تبديل الأساسات

فضاء الضرب الداخلي-الزوايا والتعامد في فضاء الضرب الداخلي