

علم الكيمياء

تاريخ الكيمياء والعلماء المشاهير

التحاضير والتجارب الكيميائية

المخاطر والوقاية في الكيمياء

اخرى

مقالات متنوعة في علم الكيمياء

كيمياء عامة


الكيمياء التحليلية

مواضيع عامة في الكيمياء التحليلية

التحليل النوعي والكمي

التحليل الآلي (الطيفي)

طرق الفصل والتنقية


الكيمياء الحياتية

مواضيع عامة في الكيمياء الحياتية

الكاربوهيدرات

الاحماض الامينية والبروتينات

الانزيمات

الدهون

الاحماض النووية

الفيتامينات والمرافقات الانزيمية

الهرمونات


الكيمياء العضوية

مواضيع عامة في الكيمياء العضوية

الهايدروكاربونات

المركبات الوسطية وميكانيكيات التفاعلات العضوية

التشخيص العضوي

تجارب وتفاعلات في الكيمياء العضوية


الكيمياء الفيزيائية

مواضيع عامة في الكيمياء الفيزيائية

الكيمياء الحرارية

حركية التفاعلات الكيميائية

الكيمياء الكهربائية


الكيمياء اللاعضوية

مواضيع عامة في الكيمياء اللاعضوية

الجدول الدوري وخواص العناصر

نظريات التآصر الكيميائي

كيمياء العناصر الانتقالية ومركباتها المعقدة


مواضيع اخرى في الكيمياء

كيمياء النانو

الكيمياء السريرية

الكيمياء الطبية والدوائية

كيمياء الاغذية والنواتج الطبيعية

الكيمياء الجنائية


الكيمياء الصناعية

البترو كيمياويات

الكيمياء الخضراء

كيمياء البيئة

كيمياء البوليمرات

مواضيع عامة في الكيمياء الصناعية

الكيمياء الاشعاعية والنووية
الأخطاء الناتجة من عملية الفصل
المؤلف:
أ. د محمد مجدي واصل
المصدر:
اسس الكيمياء التحليلية
الجزء والصفحة:
ص 411-414
2023-09-26
1752
إن عملية افصل التي تعتمد اعتمادا عاماً على عمليات الاتزان لا يمكن أن تكون عمليات فصل تامة للفصائل المتداخلة من الفصائل المراد تحليلها . وعليه فإن العاملين اللذين يجب أن يؤخذا بنظر الاعتبار في أي عملية فصل هما :
( 1 ) اكتمال عملية استرداد الأتاليت .
(2) درجة الفصل عن المكونات غير المرغوب فيها .
إن هذه العوامل يمكن أن يعبر عنها جبرياً بنسب الاسترداد( Q ( Recovery ratios . مثال ذلك ، إذا كانت X هي : كمية الأتاليت الذي استرد في الفصل وإن هي كمية X في النموذج الأصلي يمكن التعبير عن نسبة الاسترداد بواسطة المعادلة التالية:
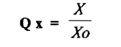
حيث أن Xo وX تمثلان الكميات الابتدائية والنهائية علي التوالي وكلما أصبحت صغيرة . كلما أصبحت عملية الفصل أفضل .
إن الاسترداد غير الكامل إلى x يؤدي دائماً إلى خطأ سالب . إن الخطأ المرافق الكامل إلي x يؤدي دائماً إلى خطأ سالب . إن الخطأ المرافق للإزالة غير التامة إلى y سوف يكون موجباً إذا كانت هذه الفصائل مشاركة للكمية المقيسة تحليلياً ويكون الخطأ سالباً إذا كانت تقلل من القيمة المعنية . ولاختيار طبيعة هذه الأخطاء دعنا نفترض أن التحليل يعتمد علي قياس قسم من الكمية M التي تتناسب مع كمية x وكمية ا في المحلول الذي يلي عملية الفصل ) أن M ربما تمثل الكتلة ، أو الحجـــم ، أو الامتصاص ، أو تيار الانتشار diffusion curront ، وهلم جرا وعليه فيمكن كتابة
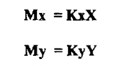
إذ أن Kx و Ky ثوابت تتناسب مع دقة القياس لكل مكون ( تكون Ky سالبة عندما تتداخل بحيث تؤدي إلي تقليل حساسية القياس إلى X )·
فإذا كانت كل من X و Y موجودة فإن قياس قيمة M تمثل مجموع المكونات Y ، X
M = Mx + My
لنفرض أن Moهي قيمة للكمية المقيسة التي يمكن الحصول عليها عندما لا يحتوي النموذج على y ، فإن :
Mo=Kx Xo
فعليه عندما يكون كلا X, Y موجودة فإن الخطأ النسبي المرافق لعملية الفصـــل يمكن أن يعبر عنه بالمعادلة التالية :

يمثل المصطلح الأول في هذه المعادلة الخطأ الذي يرافق الخسارة بـ X خــلال عملية الفصل . فعليه فإذا 99 % من X استرداد خلال عملية الفص
( 0.99 = Qx = X/Xo ) فإن خطأ نسبياً مقداره 0.01 - او % 1 - ينتج من هذا المصدر.
يأخذ المصطلح الثاني من هذه المعادلة بحساب الخطأ الناتج من الإزالة غير التامة إلي y بواسطة الفصل . إن قيمة هذا الخطأ لا تعزي فقط إلي نسبة استرداد Q ولكنها تعتمد كذلك على نسبة Yo إلي Xo في النموذج .
وعليه فإن نسبة استرداد عالية مقبولة Qx تكون مرغوبة لفصل المكونات القليلة غير المرغوب فيها x من المكون الرئيسي y . إن هذه الحالة غالباً ما تحســب فـــي التحليل الأيثري عندما تكون نسبة Yo إلى Xo في بادئ الأمر هي قدر 106 إلى 107
ويبدو أن الخطأ المستهدف في عملية الفصل يعتمد كذلك على الدقة النسبية للقياس للمكونين ( Ky/Kx ) فإن لم يتأثر هذا القياس تأثيراً كبيراً بوجود Y ( وهذه معناه ، إذا كانت Ky صغيرة ( فإن عملية الفصل النسبي غير التام تكون مناسبة لذلك التحليل . ومن جهة أخرى فإذا كان نظام القياس متساوي الحساسية لكلا x و y فقد يتطلب الأمر عملية فصل أكثر اكتمالا .