
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Watching the electrons
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المصدر:
The Feynman Lectures on Physics
الجزء والصفحة:
Volume I, Chapter 37
2024-04-20
1729
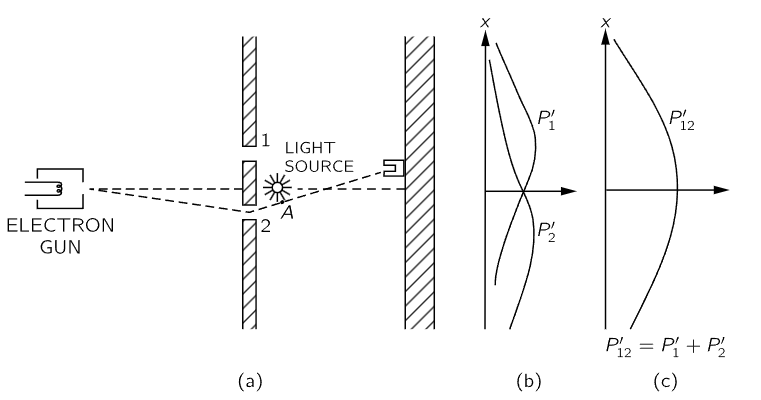
Fig. 37–4. A different electron experiment.
We shall now try the following experiment. To our electron apparatus we add a very strong light source, placed behind the wall and between the two holes, as shown in Fig. 37–4. We know that electric charges scatter light. So, when an electron passes, however it does pass, on its way to the detector, it will scatter some light to our eye, and we can see where the electron goes. If, for instance, an electron was to take the path via hole 2 that is sketched in Fig. 37–4, we should see a flash of light coming from the vicinity of the place marked A in the figure. If an electron passes through hole 1 we would expect to see a flash from the vicinity of the upper hole. If it should happen that we get light from both places at the same time, because the electron divides in half … Let us just do the experiment!
Here is what we see: every time that we hear a “click” from our electron detector (at the backstop), we also see a flash of light either near hole 1 or near hole 2, but never both at once! And we observe the same result no matter where we put the detector. From this observation we conclude that when we look at the electrons, we find that the electrons go either through one hole or the other. Experimentally, Proposition A is necessarily true.
What, then, is wrong with our argument against Proposition A? Why isn’t P12 just equal to P1+P2? Back to experiment! Let us keep track of the electrons and find out what they are doing. For each position (x-location) of the detector we will count the electrons that arrive and also keep track of which hole they went through, by watching for the flashes. We can keep track of things this way: whenever we hear a “click” we will put a count in Column 1 if we see the flash near hole 1, and if we see the flash near hole 2, we will record a count in Column 2. Every electron which arrives is recorded in one of two classes: those which come through 1 and those which come through 2. From the number recorded in Column 1 we get the probability P′1 that an electron will arrive at the detector via hole 1; and from the number recorded in Column 2 we get P′2, the probability that an electron will arrive at the detector via hole 2. If we now repeat such a measurement for many values of x, we get the curves for P′1 and P′2 shown in part (b) of Fig. 37–4.
Well, that is not too surprising! We get for P′1 something quite similar to what we got before for P1 by blocking off hole 2; and P′2 is similar to what we got by blocking hole 1. So there is not any complicated business like going through both holes. When we watch them, the electrons come through just as we would expect them to come through. Whether the holes are closed or open, those which we see come through hole 1 are distributed in the same way whether hole 2 is open or closed.
But wait! What do we have now for the total probability, the probability that an electron will arrive at the detector by any route? We already have that information. We just pretend that we never looked at the light flashes, and we lump together the detector clicks which we have separated into the two columns. We must just add the numbers. For the probability that an electron will arrive at the backstop by passing through either hole, we do find P′12=P′1+P′2. That is, although we succeeded in watching which hole our electrons come through, we no longer get the old interference curve P12, but a new one, P′12 showing no interference! If we turn out the light P12 is restored.
We must conclude that when we look at the electrons the distribution of them on the screen is different than when we do not look. Perhaps it is turning on our light source that disturbs things? It must be that the electrons are very delicate, and the light, when it scatters off the electrons, gives them a jolt that changes their motion. We know that the electric field of the light acting on a charge will exert a force on it. So perhaps we should expect the motion to be changed. Anyway, the light exerts a big influence on the electrons. By trying to “watch” the electrons we have changed their motions. That is, the jolt given to the electron when the photon is scattered by it is such as to change the electron’s motion enough so that if it might have gone to where P12 was at a maximum it will instead land where P12 was a minimum; that is why we no longer see the wavy interference effects.
You may be thinking: “Don’t use such a bright source! Turn the brightness down! The light waves will then be weaker and will not disturb the electrons so much. Surely, by making the light dimmer and dimmer, eventually the wave will be weak enough that it will have a negligible effect.” O.K. Let’s try it. The first thing we observe is that the flashes of light scattered from the electrons as they pass by does not get weaker. It is always the same-sized flash. The only thing that happens as the light is made dimmer is that sometimes we hear a “click” from the detector but see no flash at all. The electron has gone by without being “seen.” What we are observing is that light also acts like electrons, we knew that it was “wavy,” but now we find that it is also “lumpy.” It always arrives—or is scattered—in lumps that we call “photons.” As we turn down the intensity of the light source, we do not change the size of the photons, only the rate at which they are emitted. That explains why, when our source is dim, some electrons get by without being seen. There did not happen to be a photon around at the time the electron went through.
This is all a little discouraging. If it is true that whenever we “see” the electron we see the same-sized flash, then those electrons we see are always the disturbed ones. Let us try the experiment with a dim light anyway. Now whenever we hear a click in the detector, we will keep a count in three columns: in Column (1) those electrons seen by hole 1, in Column (2) those electrons seen by hole 2, and in Column (3) those electrons not seen at all. When we work up our data (computing the probabilities) we find these results: Those “seen by hole 1” have a distribution like P′1; those “seen by hole 2” have a distribution like P′2 (so that those “seen by either hole 1 or 2” have a distribution like P′12); and those “not seen at all” have a “wavy” distribution just like P12 of Fig. 37–3! If the electrons are not seen, we have interference!
That is understandable. When we do not see the electron, no photon disturbs it, and when we do see it, a photon has disturbed it. There is always the same amount of disturbance because the light photons all produce the same-sized effects and the effect of the photons being scattered is enough to smear out any interference effect.
Is there not some way we can see the electrons without disturbing them? We learned in an earlier chapter that the momentum carried by a “photon” is inversely proportional to its wavelength (p=h/λ). Certainly, the jolt given to the electron when the photon is scattered toward our eye depends on the momentum that photon carries. Aha! If we want to disturb the electrons only slightly, we should not have lowered the intensity of the light, we should have lowered its frequency (the same as increasing its wavelength). Let us use light of a redder color. We could even use infrared light, or radiowaves (like radar), and “see” where the electron went with the help of some equipment that can “see” light of these longer wavelengths. If we use “gentler” light perhaps we can avoid disturbing the electrons so much.
Let us try the experiment with longer waves. We shall keep repeating our experiment, each time with light of a longer wavelength. At first, nothing seems to change. The results are the same. Then a terrible thing happens. You remember that when we discussed the microscope, we pointed out that, due to the wave nature of the light, there is a limitation on how close two spots can be and still be seen as two separate spots. This distance is of the order of the wavelength of light. So now, when we make the wavelength longer than the distance between our holes, we see a big fuzzy flash when the light is scattered by the electrons. We can no longer tell which hole the electron went through! We just know it went somewhere! And it is just with light of this color that we find that the jolts given to the electron are small enough so that P′12 begins to look like P12—that we begin to get some interference effect. And it is only for wavelengths much longer than the separation of the two holes (when we have no chance at all of telling where the electron went) that the disturbance due to the light gets sufficiently small that we again get the curve P12 shown in Fig. 37–3.
In our experiment we find that it is impossible to arrange the light in such a way that one can tell which hole the electron went through, and at the same time not disturb the pattern. It was suggested by Heisenberg that the then new laws of nature could only be consistent if there were some basic limitations on our experimental capabilities not previously recognized. He proposed, as a general principle, his uncertainty principle, which we can state in terms of our experiment as follows: “It is impossible to design an apparatus to determine which hole the electron passes through, that will not at the same time disturb the electrons enough to destroy the interference pattern.” If an apparatus is capable of determining which hole the electron goes through, it cannot be so delicate that it does not disturb the pattern in an essential way. No one has ever found (or even thought of) a way around the uncertainty principle. So we must assume that it describes a basic characteristic of nature.
The complete theory of quantum mechanics which we now use to describe atoms and, in fact, all matter depends on the correctness of the uncertainty principle. Since quantum mechanics is such a successful theory, our belief in the uncertainty principle is reinforced. But if a way to “beat” the uncertainty principle was ever discovered, quantum mechanics would give inconsistent results and would have to be discarded as a valid theory of nature.
“Well,” you say, “what about Proposition A? It is true, or is it not true, that the electron either goes through hole 1 or it goes through hole 2?” The only answer that can be given is that we have found from experiment that there is a certain special way that we have to think in order that we do not get into inconsistencies. What we must say (to avoid making wrong predictions) is the following. If one looks at the holes or, more accurately, if one has a piece of apparatus which is capable of determining whether the electrons go through hole 1 or hole 2, then one can say that it goes either through hole 1 or hole 2. But, when one does not try to tell which way the electron goes, when there is nothing in the experiment to disturb the electrons, then one may not say that an electron goes either through hole 1 or hole 2. If one does say that, and starts to make any deductions from the statement, he will make errors in the analysis. This is the logical tightrope on which we must walk if we wish to describe nature successfully.
ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
If the motion of all matter—as well as electrons—must be described in terms of waves, what about the bullets in our first experiment? Why didn’t we see an interference pattern there? It turns out that for the bullets the wavelengths were so tiny that the interference patterns became very fine. So fine, in fact, that with any detector of finite size one could not distinguish the separate maxima and minima. What we saw was only a kind of average, which is the classical curve. In Fig. 37–5 we have tried to indicate schematically what happens with large-scale objects. Part (a) of the figure shows the probability distribution one might predict for bullets, using quantum mechanics. The rapid wiggles are supposed to represent the interference pattern one gets for waves of very short wavelength. Any physical detector, however, straddles several wiggles of the probability curve, so that the measurements show the smooth curve drawn in part (b) of the figure.

Fig. 37–5. Interference pattern with bullets: (a) actual (schematic), (b) observed.
 الاكثر قراءة في ميكانيكا الكم
الاكثر قراءة في ميكانيكا الكم
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















